[科普中国]-风压概率

风压标准要求一定概率下的最大风速，即一定重现期的年最大风速。所谓重现期，指大于某数值的最大风速平均多少年可能遇到1次。如50年一遇，它的重现期为50年。

重现期不是周期，如在1959年出现了百年一遇的大风，这并不意味着下一次将在2059年又出现。不过，使用重现期的概念是体现建筑结构的安全度。换句话说，建筑结构的安全度可用设计时采用的重现期长短来体现。重现期为50 a的风速，每1年出现超过这个风速的概率是1/50(即2%)，不超过这个风速的概率为49/50=98%。重现期为100 a的风速，每年再现的概率为1/100=1%，每年不超过这个风速概率是99/100=99%。所以，重现期长比重现期短更安全。

简介风压标准要求一定概率下的最大风速，即一定重现期的年最大风速。所谓重现期，指大于某数值的最大风速平均多少年可能遇到1次。如50年一遇，它的重现期为50年。

重现期不是周期，如在1959年出现了百年一遇的大风，这并不意味着下一次将在2059年又出现。不过，使用重现期的概念是体现建筑结构的安全度。换句话说，建筑结构的安全度可用设计时采用的重现期长短来体现。重现期为50 a的风速，每1年出现超过这个风速的概率是1/50(即2%)，不超过这个风速的概率为49/50=98%。重现期为100 a的风速，每年再现的概率为1/100=1%，每年不超过这个风速概率是99/100=99%。所以，重现期长比重现期短更安全。1

X分布函数风速极值的重复发生，可以利用极值理论进行计算。每年最大风速Xmax，它是一个随机变量，不同年代出现的最大风速值不同。以F(x)代表X小于Xmax的概率，称为X分布函数。

研究最大风速的问题，首先确定F(x)的线型。关于线型的确定，国内外进行了很多工作。归纳起来主要有两方面，一方面从统计理论上确定年最大风速应服从的概率线型，然后从实际资料确定其参数，如极值分布线型另一方面，从经验概率上确定年最大风速分布线型，然后从实际资料确定其参数，如皮尔逊线型族。目前国内外，在计算风压时，基本上采用极值分布线型。从统计学理论导出随机变量的极值的概率分布称极值分布。以风速为例说明极值分布的意义。

从每年的风速记录中挑出每年的最大风速，许多个年最大风速必具有一概率分布，属于极大值的分布。1

极值I型极值分布在气候正常时用的是I型极值分布(又称双指数分布)

原始分布属指数型，其极大值X的分布应属I型分布，其分布函数：

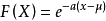
检验风速的理论分布与经验分布的适合度，一般采用科尔莫洛夫检验或w检验。1

本词条内容贡献者为:

刘勇 - 副教授 - 西南大学资源环境学院