[科普中国]-艾佛森括号

在数学中，以Kenneth E. Iverson命名的“艾佛森括号”，是一种用方括号记号，如果方括号内的条件满足则为1，不满足则为0。

简介在数学中，以Kenneth E. Iverson命名的“艾佛森括号”，是一种用方括号记号，如果方括号内的条件满足则为1，不满足则为0. 更确切地讲，

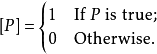此处P是一个可真可假的命题。该记号由Kenneth E. Iverson在他的编程语言APL中引进，而特别使用方括号则是由高德纳倡导的，目的是避免含括号的表达式中的歧义。1

用途艾弗森括号通过自然的映射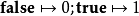 将布尔值转化为整数值，这就允许计数被表示为和式。例如，计数与小于n且正整数n互质的正整数的个数的欧拉函数可以表示为

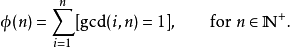
更一般地，此记号使得将和式和积分式中繁多的条件移入并成为被加（积）项的一个因子成为可能。这将减少累加记号周围的空间，更重要的是这允许运算更加代数化。例如，

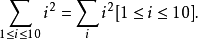
另一个例子是化简带特例的方程，例如公式

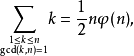对一切n> 1有效，但是右边有12对于n= 1。为了得到一个一切正整数n都成立的恒等式，可以利用艾弗森括号补充等式：

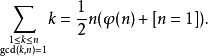
特例克罗内克函数：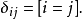

符号函数和单位阶跃函数：

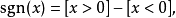
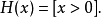
最值与绝对值：

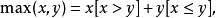
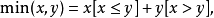
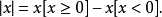上下取整函数：

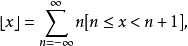
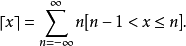
麦考利括号可被表示为

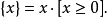
实数的三分律等价于下面的恒等式：

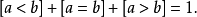
另见麦考利括号

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学