对给定的覆盖单元集F,设图G所有边(点)覆盖所构成的集族为J,对每一覆盖S∈J,将一个单项式X(S)定义为Πα∈Swα,进而对图G赋以一个多项式P(G)为ΠS∈JX(S),这个P(G)便称为图G在F之下的“边(点)覆盖多项式”。
基本介绍考察有向(无向)简单图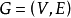 ,其中
,其中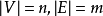 ,必要时也可以考虑有自环(loop)的有向图,今后分别以V(S)及E(S)表示子图S的顶点集及边集;记号
,必要时也可以考虑有自环(loop)的有向图,今后分别以V(S)及E(S)表示子图S的顶点集及边集;记号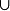 表示子图的并运算。
表示子图的并运算。
相关定义定义1 取定图G的一个子图族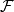 ;对其中每一个子图
;对其中每一个子图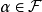 ,赋以某一整环R中之元
,赋以某一整环R中之元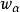 ,作为它的度量,这样一个具有度量的子图族
,作为它的度量,这样一个具有度量的子图族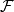 便称为“覆盖单元集”;其中每一个子图α 称为“(覆盖)单元”。
便称为“覆盖单元集”;其中每一个子图α 称为“(覆盖)单元”。
定义2 对于不含全不连通子图的覆盖单元集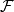 而言,图G的一个“边覆盖”,是指由若干个无公共边的单元所组成的集合
而言,图G的一个“边覆盖”,是指由若干个无公共边的单元所组成的集合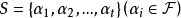 ,使得
,使得
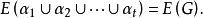 换言之,
换言之,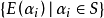 构成边集E(G)的一个划分。
构成边集E(G)的一个划分。
定义2’ 对给定的覆盖单元集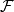 而言,图G的一个“点覆盖”,是指由若干个无公共顶点的单元所组成的集合
而言,图G的一个“点覆盖”,是指由若干个无公共顶点的单元所组成的集合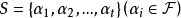 ,使得
,使得
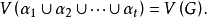 换言之,
换言之,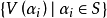 构成顶点集V(G)的一个划分。
构成顶点集V(G)的一个划分。
点覆盖多项式的定义定义3对给定的覆盖单元集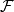 ,设图G所有边(点)覆盖所构成的集族为
,设图G所有边(点)覆盖所构成的集族为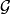 ,对每一覆盖
,对每一覆盖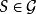 ,赋以一个单项式
,赋以一个单项式
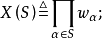 进而对图G赋以一个多项式
进而对图G赋以一个多项式
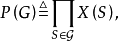 这个P(G)便称为图G在
这个P(G)便称为图G在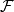 之下的“边(点)覆盖多项式”。
之下的“边(点)覆盖多项式”。
下文始终采取“空和为零,空积为1“的习惯约定,因此,当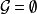 时,P(G)=0,当G=
时,P(G)=0,当G=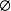 (空图)时,只有一个覆盖
(空图)时,只有一个覆盖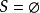 ;而
;而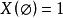 ,所以
,所以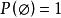 。其次,在边覆盖多项式的情况,增减一些孤立顶点时边覆盖不变,因而多项式亦不变;故此时不妨假定图G并无孤立顶点。
。其次,在边覆盖多项式的情况,增减一些孤立顶点时边覆盖不变,因而多项式亦不变;故此时不妨假定图G并无孤立顶点。
举例分析下面来看一些例子。
1.圈多项式
在无向图的情况,设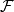 由G中所有的K1(一点生成子图)、K2(一边生成子图)及初级圈(点数≥3)所构成,R为实数域上的多项式环,由此产生出的点覆盖多项式通常称为“圈多项式”,特别当单元K1的度量为
由G中所有的K1(一点生成子图)、K2(一边生成子图)及初级圈(点数≥3)所构成,R为实数域上的多项式环,由此产生出的点覆盖多项式通常称为“圈多项式”,特别当单元K1的度量为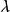 (未定元),K2的度量为-1,其它初级圈的度量为-2时,点覆盖多项式
(未定元),K2的度量为-1,其它初级圈的度量为-2时,点覆盖多项式
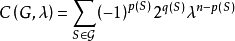 就是熟知的特征多项式,其中p(S)为S中有边的单元数,q(S)为S中的圈数。
就是熟知的特征多项式,其中p(S)为S中有边的单元数,q(S)为S中的圈数。
2.子图多项式
当G为无向图,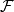 由G的一切连通子图所构成时,图G在
由G的一切连通子图所构成时,图G在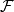 之下的点覆盖多项式称为“子图多项式”,而当单元
之下的点覆盖多项式称为“子图多项式”,而当单元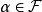 的度量
的度量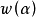 不同时,可得一些特殊的多项式,例如:
不同时,可得一些特殊的多项式,例如:
(1°) 对每一单元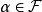 ,赋以度量
,赋以度量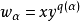 ,其中
,其中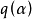 为连通子图α 的圈秩,那么图G在这种覆盖意义下的多项式
为连通子图α 的圈秩,那么图G在这种覆盖意义下的多项式
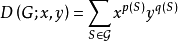 就是双色多项式,其中p(S)及q(S)分别表示由S的单元的并所构成的支撑子图的分图数及圈秩
就是双色多项式,其中p(S)及q(S)分别表示由S的单元的并所构成的支撑子图的分图数及圈秩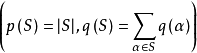 。
。
(2°) 若令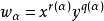 ,其中
,其中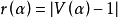 为连通子图α 的秩,则
为连通子图α 的秩,则
 就是秩多项式,其中,
就是秩多项式,其中,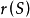 表示由S所成的支撑子图的秩。
表示由S所成的支撑子图的秩。
(3°) 若令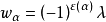 ,其中
,其中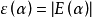 为连通子图
为连通子图 的边数,则
的边数,则
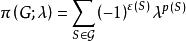 就是色多项式,事实上,记
就是色多项式,事实上,记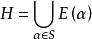 ,并以
,并以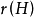 表示H的生成子图的秩,则上式可改写为
表示H的生成子图的秩,则上式可改写为
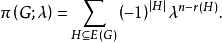 这就是色多项式的展开式(极易由容斥原理推出)。
这就是色多项式的展开式(极易由容斥原理推出)。
4.匹配多项式
设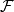 由G中所有子图K1及K2所构成,它们的度量分别为x及y,由这种单元组成的点覆盖S就是图G的“匹配”(matching);它对应的单项式为
由G中所有子图K1及K2所构成,它们的度量分别为x及y,由这种单元组成的点覆盖S就是图G的“匹配”(matching);它对应的单项式为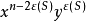 ,其中
,其中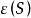 为S中单元K2的数目(边数),于是
为S中单元K2的数目(边数),于是
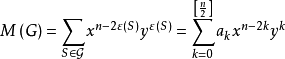 就是图G的匹配多项式,其中
就是图G的匹配多项式,其中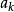 为k边匹配的数目1。
为k边匹配的数目1。
基本定理设图G= (V,E)在单元集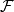 之下的边(点)覆盖多项式为P(G),下面将给出这两类多项式的一般消去定理。
之下的边(点)覆盖多项式为P(G),下面将给出这两类多项式的一般消去定理。
定义4 对任意的顶点子集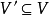 及边子集
及边子集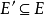 ,二元组
,二元组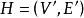 称为G的“伪子图”。
称为G的“伪子图”。
当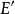 中每条边所关联的顶点均属于
中每条边所关联的顶点均属于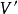 时,
时,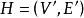 就是通常意义的子图,
就是通常意义的子图,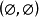 将简记为
将简记为 。
。
定义5 给定G的一个伪子图H,图G关于H的部分边(点) 覆盖SH,是指由若干个无公共边(点)的单元所组成的集合,这些单元的并包含了H的全部顶点和边,且每个单元都至少含有H的一个顶点或一条边。
对于图G的一个边(点)覆盖S 而言,如果S覆盖着H的点和边,则将S 中含有H的顶点或边的单元取出来,这样构成的子集SH一定是关于H的部分覆盖,即有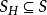 ,但反过来说,一个部分覆盖却不一定能成为某个覆盖的子集(它未必能添上一些单元后构成G的覆盖)。
,但反过来说,一个部分覆盖却不一定能成为某个覆盖的子集(它未必能添上一些单元后构成G的覆盖)。
定义6 对部分边(点)覆盖 而言,其相应的单项式定义为
而言,其相应的单项式定义为
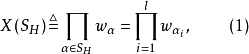
特别当 ,因而
,因而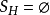 时,
时, 。
。
此外,我们记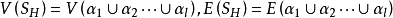 。
。
现在,分两种情况讨论。
边覆盖多项式的消去定理定义7 一个关于H的部分边覆盖SH称为极大的,如果不存在以它为真子集的另一个关于H的部分边覆盖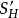 。
。
命题 对任一个边覆盖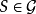 ,由其中所有含有H的顶点或边的单元所构成的部分边覆盖SH一定是极大的。
,由其中所有含有H的顶点或边的单元所构成的部分边覆盖SH一定是极大的。
证明: 设 是按上述方式导出的部分边覆盖,那么H中的边(
是按上述方式导出的部分边覆盖,那么H中的边(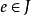 )及H中的顶点所关联的边(
)及H中的顶点所关联的边(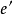 的端点
的端点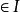 )均被SH的单元所覆盖;而任一单元均非孤立点,所以不存在这样的单元,它与SH的单元无公共边而又包含H的顶点或边,故SH为极大的。
)均被SH的单元所覆盖;而任一单元均非孤立点,所以不存在这样的单元,它与SH的单元无公共边而又包含H的顶点或边,故SH为极大的。
定理1 设图G在单元集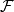 之下的边覆盖多项式为P(G),并设
之下的边覆盖多项式为P(G),并设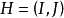 为G的一个伪子图,则
为G的一个伪子图,则
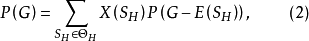 其中
其中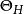 为G关于H的一切极大的部分边覆盖的集合。
为G关于H的一切极大的部分边覆盖的集合。
点覆盖多项式的消去定理取定图G的一个伪子图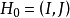 ,考察由它除去一些边所成的伪子图H的集合
,考察由它除去一些边所成的伪子图H的集合
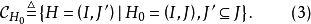 对于每一个
对于每一个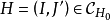 ,又考察部分点覆盖的集合
,又考察部分点覆盖的集合
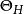
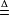 {部分点覆盖
{部分点覆盖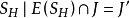 }. (4)
}. (4)
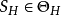 就是G关于H的部分点覆盖,它的单元包含J' 的边,而不包含
就是G关于H的部分点覆盖,它的单元包含J' 的边,而不包含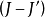 的边。为更明显起见,对于
的边。为更明显起见,对于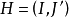 ,我们令
,我们令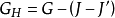 。那么,
。那么,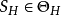 就是图GH关于H的部分点覆盖。
就是图GH关于H的部分点覆盖。
定理2 设图G在单元集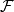 之下的点覆盖多项式为P(G),并设
之下的点覆盖多项式为P(G),并设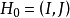 为G的一个伪子图,则
为G的一个伪子图,则
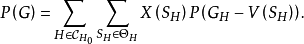 其中集合
其中集合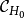 及
及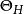 分别由(3)(4)式所定义1。
分别由(3)(4)式所定义1。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国