与一元函数的极限相类似,二元函数的极限同样是二元函数微积分的基础。但因自变量个数的增多,导致二元函数的极限要比一元函数的极限复杂很多。求累次极限实质上是求两次一元函数的极限,因此,累次极限又称二次极限。需要注意的是:累次极限与重极限是两个不同的概念,它们的存在性没有必然的蕴含关系。
定义和例子定义1设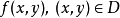 ,
,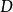 在
在 轴、
轴、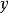 轴上的投影分别为
轴上的投影分别为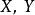 ,即
,即
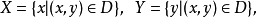
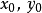 分别是
分别是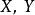 的聚点。若对每一个
的聚点。若对每一个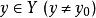 ,存在极限
,存在极限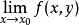 ,它一般与
,它一般与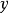 有关,故记作
有关,故记作
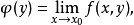 如果进一步还存在极限
如果进一步还存在极限
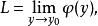 则称此极限
则称此极限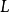 为
为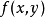 先对
先对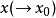 ,后对
,后对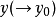 的累次极限1,记作
的累次极限1,记作
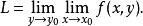 类似地可以定义先对
类似地可以定义先对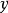 后对
后对 的累次极限
的累次极限
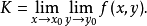
对于两个自变量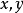 同时以任何方式趋于
同时以任何方式趋于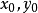 ,即
,即
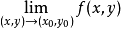 这种极限也称为重极限。
这种极限也称为重极限。
累次极限与重极限是两个不同的概念,它们的存在性没有必然的蕴含关系。下面两个例子将说明这一点。
例1设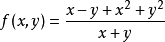 ,它关于原点的两个累次极限分别为
,它关于原点的两个累次极限分别为
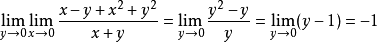 与
与
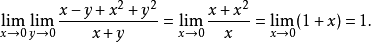 当沿斜率不同的直线
当沿斜率不同的直线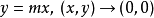 ,容易验证所得极限也不同。因此该函数的重极限不存在。
,容易验证所得极限也不同。因此该函数的重极限不存在。
例2设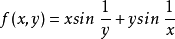 ,它关于原点的两个累次极限都不存在。这是因为对任何
,它关于原点的两个累次极限都不存在。这是因为对任何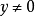 ,当
,当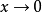 时
时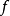 的第二项不存在极限。同理,对任何
的第二项不存在极限。同理,对任何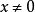 ,当
,当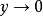 时
时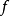 的第一项也不存在极限。但是由于
的第一项也不存在极限。但是由于
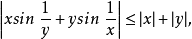 故
故 的重极限存在,且
的重极限存在,且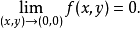
重极限与累次极限之间的联系定理1若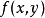 在点
在点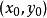 存在重极限
存在重极限
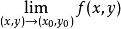 与累次极限
与累次极限
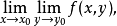 则它们必相等。
则它们必相等。
推论1若累次极限
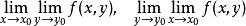 和重极限
和重极限
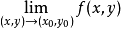 都存在,则三者相等。
都存在,则三者相等。
推论2若累次极限

存在但不相等,则重极限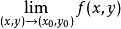 必不存在。
必不存在。
定理1保证了在重极限与一个累次极限都存在时,它们必相等,但它们对另一个累次极限的存在性却得不出什么结论。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国