[科普中国]-一般项级数

数项级数的收敛性问题是数学分析中研究的基本内容之一。数项级数主要分为正项级数和一般项级数，一般项级数的收敛性判别问题要比正项级数复杂。在此，我们只讨论某些特殊类型的级数的收敛性问题，比如交错级数，绝对收敛级数，条件收敛级数。

交错级数若级数的各项符号正负相间，即

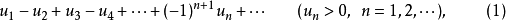则称（1）为交错级数。

对于交错级数，有下面常用的判别法。

定理1（莱布尼茨判别法）若交错级数（1）满足下述两个条件：

（i）数列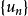 单调递减；

（ii）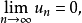

则级数（1）收敛1。

推论1若级数（1）满足莱布尼茨判别法的条件，则收敛级数（1）的余项估计式为

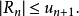对于下列交错级数应用莱布尼茨判别法检验，容易检验它们都是收敛的。

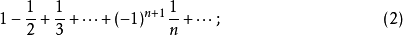
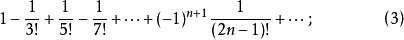
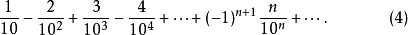
绝对收敛级数及其性质若级数

各项绝对值所组成的级数

收敛，则称原级数（2）为绝对收敛级数。

定理2绝对收敛级数一定收敛1。

例1级数

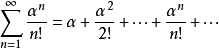的各项绝对值所组成的级数是

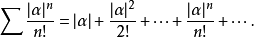应用比式判别法，对于任何实数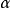都有

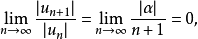因此，所考察的级数对任何实数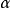都绝对收敛。

若级数（5）收敛，但级数（6）不收敛，则称级数（5）为条件收敛级数。

例如级数（2）是条件收敛，而级数（3）、（4）则是绝对收敛。

全体收敛的级数可分为绝对收敛级数与条件收敛级数两大类。

阿贝尔判别法和狄利克雷判别法下面讨论级数

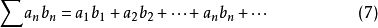收敛性的判别法。

定理3（阿贝尔判别法）若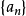为单调有界数列，且级数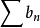收敛，则级数（7）收敛。

定理4（狄利克雷判别法）若数列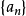单调递减，且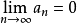，又级数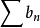的部分和数列有界，则级数（7）收敛。

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学