[科普中国]-波动方程分析

波动方程分析方法可用来进行动力验桩，在已知桩锤、打桩机和桩土信息的基础上计算桩的承载力。它取代了用收锤时的锤击数来预测承载力的动力打桩公式，并在准确的土信息的基础上预测打桩过程。

概念波动方程就是描述波动现象的偏微分方程。打桩时，锤击能量克服土对桩的阻力而把桩击入土中。对于直径大、长度长的桩，按惯用的动力打桩公式预测桩的承载力等问题已不能适应。其原因是，它们把打桩过程看成是两个绝对刚体自由碰撞问题，认为锤击能量瞬间就传递到桩底，但实际上打桩的能量是以一种应力波的方式向下传递，所以用波动方程能给打桩提供较合理的分析。1

波动方程有限差分正演模拟误差来源分析波动方程有限差分模拟方法是波场数值模拟中最为流行的方法之一，但在用有限差分方法求解波动方程时，常常会产生不期望的数值频散或称网格频散，导致数值模拟结果分辨率的降低。所谓数值频散实质上是一种因离散化求解波动方程而产生的伪波动，它是有限差分方法求解波动方程时所固有的本质特征，无法避免，但是可以通过合适的参数选择和适当的数学方法予以减小。

在做有限差分波动方程正演数值模拟时主要是要综合考虑差分格式、震源的选择、边界条件的处理等问题。这些问题能否正确处理直接影响正演模拟结果的正确性，并且误差是由这些因素综合影响，如果其中任何一个问题得不到恰当地处理，都会给正演结果带来误差。

高阶有限差分法在做波动方程正演模拟时，具有计算速度快、频散较小的特征，在做有限差分正演过程中必须注意震源、边界条件等因素的影响，否则就会出现意想不到的结果。总体来说选择较小的空间和时间步长能保证结果的正确性，但是时间和空间的步长的减小必定增加运算的时间，因此要保证运算速度与精度就必须处理好各个参数之间的关系。2

波动方程分析法在动力验桩中的应用长期以来，建筑工程界广泛使用动力打桩公式来确定桩的静承载力。由于打桩公式是从能量守恒原理以及自由体的碰撞原理推导出来的，未考虑应力波在桩身中传播的过程，因而有较多的经验的成分。1960年，Smith EAL第1次将描述波在杆中传播的波动方程的数值解方法应用于实际的打桩分析中，但 Smith 法的主要缺点是缺少土的特性描述。1964年，美国的Case技术学院开始对桩基应力波检测进行系统的、大规模的研究，1975年，他们提出了两种波动方程分析方法，即Case法和CAPWAP法。从此，利用波动方程分析方法进行动力验桩得到了不断发展。

Smith法Smith法是将锤、垫层、桩帽和桩以及桩周土看作一个系统，并用质量- 弹簧系统来表示。无论对桩尖土阻力或桩周土阻力，Smith法均采用粘弹塑性数学模型来描述。在土的变形过程中，首先是发生弹性变形，其最大弹性位移用q表示。在位移超过q时，土将产生塑性流动，其应力保持不变，称为极限应力或阻力Ru。对于土的动阻力 Rd，假设服从牛顿粘滞定律，其阻力与质点速度成正比。

CAPWAP法Case法和CAPWAP法这两种方法的基本原理是一致的，即以重锤在桩顶冲击产生一个足够强的应力波沿桩身向下传播。在这个过程中，波所通过的部分，桩身经受了较高的压缩变形，产生了较大的向下质点位移，因而产生了一个瞬变的摩擦力。由于这个摩擦力是瞬变的力，它将在桩身中和桩周土中各激发出两个波。桩本身是一个波导体，在桩身中所激发出的两个波，一个是沿桩身向上传播的压缩波，它到达桩顶时被传感器记录下来；另一个是沿桩身向下传播的拉伸波，经桩底反射后也返回桩顶，其响应也被传感器记录下来。随着波阵面的不断向下运动，所产生的摩阻力信息也不断地通过这些波沿桩身传向桩顶。这样一来，摩阻力沿桩身的变化就直接反映到了桩顶波响应随时间的变化中。

研究结论利用波动方程分析方法进行动力验桩开始增多，这种方法在准确的土信息的基础上预测打桩过程，计算桩的承载力，克服了长期以来使用动力打桩公式确定桩的承载力时所具有的较多的经验成分。

Smith法的主要缺点是缺少土的特性描述。Case法和CAPWAP法虽然解决了这一问题，但其自身也有一些缺点。在CAPWAP法的计算中，每一次迭代都需要修正相对应的所有桩单元的桩周土的土性参数，并重新求解波动方程。如果桩单元较多(每个桩单元相对应 3个土性参数)，几十个土性参数同时调整是非常困难的，需要一定的经验和相当的技术知识基础。同时，CAPWAP法多次的求解过程也需要花费很多的时间。Case法是一个简化的分析方法，它建立在许多的假定的基础上，因而所得结果的误差较大。3

时栅的波动方程分析与行波形成新方法时栅经多年研究己取得重要突破。在产品化过程中逐渐凸现的问题是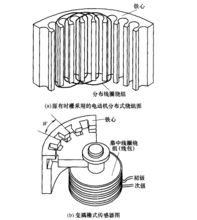：以往采用的旋转磁场是基于传统交流电动机的定子绕组而得到的。电动机作为动力装置，对绕组均分性要求不高，而时栅虽然比光栅的加工精度要求低得多，但作为精密检测元件仍然具有一定的精度指标。此外，从原理上说，除了“旋转磁场切割金属导体”的方法以外，还有没有别的行波形成方法? 为此需进一步对时栅的波动方程进行分析，探索新的行波形成方法，以加深对“时空转换”的认识并进一步降低对精密机械加工的依赖和成本。

新方案的优势及启示在弄清楚了最终需要的是能实现时空转换的电行波以及电行波的形成机理后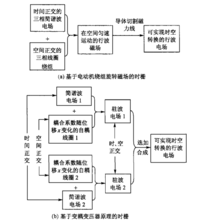，就寻求一种尽可能简便的电行波形成方式，这里提出一种利用式AsinαBcosβ+ AcosαBsinβ=ABsin（α+β）=Ksin（α+β）直接形成电行波的方法。当α为时间自变量，β为空间自变量，上式就是一个典型的行波表达式。

上述方案可以很好地解决前述时栅产品化过程存在的问题。

（1）时栅的原始机械精度不再依赖线圈分布的均匀性即等分精度，转而依赖齿的等分精度，而依靠一般的线切割或切齿加工或浇铸加工都可以保证图1端面齿的等分精度。换言之，图1所示分布线圈是一圈圈零散的线束，精度很难控制，而集中线圈加分齿的精度则容易保证。

（2） 图1b所示的集中线包绕制比图1a的分布线圈绕制简单得多，工艺大大简化，成本更低。

（3）此方案的研究思想已跳出电动机绕组旋转磁场的思路，而利用驻波电场直接合成行波电场，这为获取行波电场开辟了一条新路。两种方式在原理上的区别如图2所示。

研究结论（1）通过对场式时栅波动方程的分析，尤其是对电行波和磁行波的分析，可以得到一个全新的重要结论：磁行波和电行波虽然数学表达式完全相同，其物理意义却截然不同。前者是在空间轴上的前进和后移，后者是在时间轴上的超前和滞后。据此结论，可以加深对时空坐标转换方法、信号产生机理的认识，进而构思出更加巧妙合理和更新颖的传感器结构形式。

（2）根据上述研究，明确时空转换的最终目的是要得到一个电行波(时间行波)。于是提出了一种不同于旋转磁场方法，而用变祸合变压器原理的两路驻波来直接合成电行波的新方法。研究思路进一步打开，设计的时栅结构形式更简单合理，有利于加速成果的产品化进程。4

本词条内容贡献者为:

何星 - 副教授 - 上海交通大学