[科普中国]-微分小的变化

在数学中，微分是对函数的局部变化率的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时，函数的值是怎样改变的。当某些函数f的自变量x有一个微小的改变h时，函数的变化可以分解为两个部分。一个部分是线性部分，另一部分是比h更高阶的无穷小，这种表示方法成为微分法。

而微分变量有时会发生改变，我们把微分变量变化的多少称为微分的变化。微分变化的少称为微分小的变化。

简介编辑

在古典的微积分学中，微分被定义为变化量的线性部分，在现代的定义中，微分被定义为将自变量的改变量

映射到变化量的线性部分的线性映射。这个映射也被称为切映射。给定的函数在一点的微分如果存在，就一定是唯一的。

在数学中，微分是对函数的局部变化率的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时，函数的值是怎样改变的。当某些函数的自变量有一个微小的改变时，函数的变化可以分解为两个部分。一个部分是线性部分：在一维情况下，它正比于自变量的变化量，可以表示成和一个与无关，只与函数及有关的量的乘积；在更广泛的情况下，它是一个线性映射作用在上的值。另一部分是比更高阶的无穷小，也就是说除以后仍然会趋于零。当改变量很小时，第二部分可以忽略不计，函数的变化量约等于第一部分，也就是函数在处的微分，记作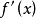 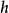或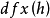 。如果一个函数在某处具有以上的性质，就称此函数在该点可微[1]1。

不是所有的函数的变化量都可以分为以上提到的两个部分。若函数在某一点无法做到可微，便称函数在该点不可微。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学