[科普中国]-非线性弹性模量

非线性弹性模量可用来代替弹性模量，对弹性介质中的波速公式作修正。将波速与应力的多值函数关系转化成波速作为应变(或密度)的单值函数。同时考虑水饱和对非线性弹性模量和波速的影响，得出速度与应变拟合关系曲线。实验数据和理论曲线有较好的一致性。

概念对于非线性弹性模量基础上双模量矩形板来说，随着非线性刚度系数的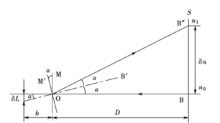增大双模量矩形板中心的挠度也逐渐变小，而且相同条件下非线性弹性基础上双模量矩形板中心的挠度要小于线性弹性基础上双模量矩形板中心的挠度。非线性基础上拉压弹性模量不同矩形板中心挠度的计算不宜采用相同弹性模量经典薄板理论，而应该采用双模量薄板弹性理论。由于非线性基础上拉压弹性模量不同矩形板的弯曲变形微分方程是非线性的，因此难以求得其精确解析解，所以采用Kantorovich和Galerkin联合法研究非线性基础上拉压弹性模量不同矩形板弯曲挠度，不但计算简便而且计算精度也较高。1

土体非线性弹性模量简易计算方法研究背景土是地壳表层的整体岩石经过物理与化学风化作用后的产物，是由固相、液相和气相组成的三相分散体系。长久以来，国内外已经建立的地基土的模型已不下数百个，但真正能反映土体真实面目的寥寥无几。由于土体本身太复杂，全面地考虑土体的本构关系，则其模型参数将会因为太多而缺乏实用性。因此，从实用角度出发，建立简易的(包括形式和参数的可得到性)、能够反映研究问题主要矛盾的典型模型是十分必要的。

土体的变形模量根据弹性模量和变形模量的关系，可得土体的变形模量如下： 。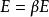

其中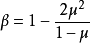 ，μ为土体的泊松比，它随土的种类及结构性强弱而取不同的值，一般地说，砂性土μ=0.2-0.25，粘性土μ=0.25-0.42，理想刚体由于无侧向变形μ=0，饱和土μ=0.5。关于弹性模量和变形模量的比值，理论上说，当μ从0(理想刚体)变化到0.5(理想的塑性体)时，β从1变化到0，但是实测资料表明，理论比值与实测比值存在较大的差异，而这种差异又随土的种类与结构强弱而变化，结构性强的老年土同拘差异较大，反之结构性弱的新近沉积的粘土则较接近理论值。

研究结论研究根据弹性模量和变形模量曲线的关系，建立了一个土体非线性弹性模量简易计算方法，并将其应用于某实际工程，计算结果表明本文的方法更符合实际。尽管利用本文的简易计算方法进行沉降计算的结果比较接近于实测沉降预估值，相对于传统的计算有极大的改进，但是二者仍然有一定的差距。分析产生偏差的产生可知，这主要是由于土体受到了较大的扰动，地质报告提供的参数偏小，计算沉降量偏大等原因造成的。因此，土样采集时尽可能少的扰动土体，保持土体本身物理力学性质的稳定性，使沉降计算时取用的土体物理力学指标能够真实的反映土体的本来性质，这是达到理论计算值和实测沉降预估值相接近的一个十分重要的前提条件。2

非线性弹性模量对波速影响的实验研究地球表层的岩石和土壤含有大量的孔隙和裂缝，可以认为是一种松散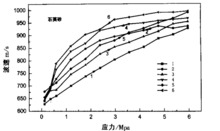介质，具有非线性弹性的特征。在循环应力的作用下，介质的非线性弹性使应力一应变曲线变成滞回圈。对此问题，MaCall利用P—M模型，对滞回曲线的产生和对波速的影响进行了研究。同时也对非线性弹性对波的频散，波形的畸变等问题进行了理论推导。而Meagan对非线性弹性波传播进行了实验研究。在他们的研究中，应力或深度或速度作为参量是相对固定的。在波的传播过程中，由于波的振幅变化，使应力、应变和模量也产生了微小的非线性变化，从而导致了波的频散、畸变和衰减等一系列复杂现象。

实验研究主要是考虑压力或深度作为自变量且大幅度变化时对波速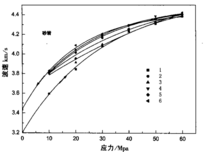所产生的影响，特别是在循环应力的条件下波速的变化规律。波速是介质的重要参数，它也受到非线性弹性的明显影响，使得波速-应力曲线与应力-应变曲线相似，也变成了滞回圈。波速成为压力的多值函数，给实际问题的处理带来了不确定性。因此我们希望能将速度对应力的多值函数转化为速度对某参量的单值函数。

用实验的方法，通过测量得到应力、应变、波速等有关参数，对非线形模量与应变的关系作了非线性拟合；用非线性模量来代替弹性模量，对弹性介质中的波速公式作了修正。将波速转化成应变(或密度)的单值函数。

实验结果图1和图2显示，速度是应力的多值函数。速度不仅与应力大小有关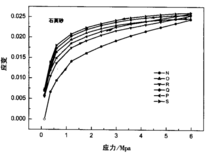，还与应力变化的方向和循环次数有关。相应于应力的每一个循环，波速也产生一个循环。在每一个循环中，卸载时的波速高于加载时的波速。而后一次循环的波速要高于前一次循环的波速，表示介质在不断被压实，而且产生了应变相对于应力的延迟或滞后。

石英砂的应力一应变曲线如图3所示。应力应变的关系是非线性的。每次应力循环时都产生了残余应变。其大致形状与速度一应力曲线相似。由于速度是应力的多值函数，给实际问题的处理带来了不确定性，因此我们希望能将速度对应力的多值函数转化为速度对应变的单值函数。

石英砂对非线性模量和波速的影响先通过活塞上的小孔使石英砂处≥于水饱和状态，然后再进行循环加卸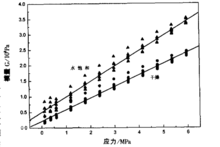载实验。因为孔隙中充满了水，使得介质较难压缩。图4是石英砂处于干燥和水饱和两种状态下的模量与应力的关系。模量随应力的变化与随应变的变化不同，近似于直线，但都随应力增加而增加。水饱和时的模量与干燥状态相比有明显的提高，而且随应力的增加速率更快。同时，在水饱和的条件下，波速也有明显的提高。由于不断缓慢排水的缘故，波速测量精度较低，数据比较分散，但大体上还是与计算拟合曲线相近。

讨论与结论地球表面的介质，如岩石和土壤。在实际工作中，可采用四种不同的模型来进行研究，即线性弹性体、非线性弹性体、塑性体和粘弹体。后三种模型，在循环应力作用下，都会产生应力一应变的滞回圈。本文采用的是非线性弹性体模型。在应力由上升转为下降时，由于应变的滞后，由应力差与应变差之比定义的模量会出现突变。这是由于裂纹的打开和关闭压力不同所造成的。在P—M模型中有较为详细的讨论。

模量随应力的突变给波速的计算带来了困难，但由于模量相对于应变是连续的，是不变的，因此用应变来替代模量和应力，非弹性模量与应变的关系。水饱和将使介质变硬，与干燥状态相比，模量不但数值大，而且上升速率快。但波速与应变的单值函数依然存在，只是常数C和B的值有所不同。利用本文的有关公式，可通过岩石样品的应力应变曲线来预测其波速在不同压力状态或不同深度时的变化。3

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所