[科普中国]-有效应力破坏包线

莫尔-库伦强度理论认为材料破坏是剪切破坏，在破坏面上的剪应力是法向应力的函数。由此函数关系所确定的曲线称为莫尔破坏包线1。由抗剪强度有效应力公式作出的莫尔破坏包线就称为有限应力破坏包线。

有效应力有效应力强度参数土的抗剪强度有两种表达方法，一种是以总应力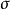 表示剪切破坏面上的法向应力，抗剪强度表达式即为库伦公式，称为抗剪强度总应力法，相应的库伦公式中的c、φ称为总应力强度参数；另一种以有效应力 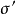表示剪切破坏面上的法向应力，其中库伦公式的修改式称为抗剪强度有效应力法，相应的库伦公式的修改式中的c'、φ'称为有效应力强度参数。

公式1773年C.A.库伦（Coulomb）根据砂土的试验，将土的抗剪强度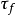 （kPa）表达为滑动面上法向总应力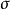（kPa）的函数，即：

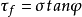
以后又提出了适合粘性土的更普遍的表达式：

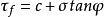
式中，c——土的粘聚力（内聚力）kPa；

φ——土的内摩擦角度。

上两式统称为库伦公式，或库伦定律，c、φ称为抗剪强度参数。

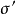长期的实验研究指出，土的抗剪强度不仅与土的性质有关，还与试验时的排水条件、剪切速率、应力状态、应力历史等许多因素有关，其中最重要的是试验时的排水条件，根据K·太沙基（Terzaghi）的有效应力概念，土体内的剪应力只能由土的骨架承担，因此，土的抗剪强度 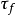应表示为剪切破坏面上的法向有效应力的函数，库伦公式应修改为：

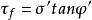
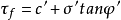
式中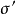 ——剪切破坏面上的法向有效应力，单位kPa；

c'——有效粘聚力，单位kPa；

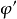——有效内摩擦角，单位度。

上述修改式便称为抗剪强度有效应力法，相应的库伦公式的修改式中的c'、φ'称为有效应力强度参数。

莫尔-库伦强度理论1910年，O.莫尔提出材料的破坏是剪切破坏，当任一平面的剪应力等于材料的抗剪强度时该点就发生破坏，并提出在破坏面上的剪应力，即抗剪强度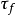 ，是该面上的法向应力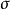的函数，即：

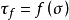
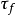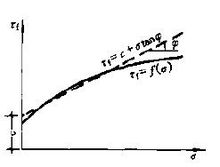
这个函数在-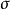坐标中是一条曲线，称为莫尔破坏包线，或称抗剪强度包线，如图1所示。莫尔包线表示材料受到不同应力作用达到极限状态时，剪切破坏面上法向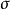应力和剪应力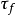的关系。理论分析和实验都证明，莫尔理论对土比较合适，土的莫尔破坏包线通常可以近似的用直线来替代，如图1虚线所示，该直线方程就是库伦公式表达的方程，由库伦公式表示莫尔破坏包线的强度理论，称为莫尔-库伦强度理论。

所以抗剪强度有效应力的表达式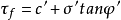所对应的莫尔破坏包线就是有效应力破坏包线。2

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所