工程中常用沉降计算大多根据压缩试验所得的e-p或e-logp曲线进行计算,并以经验系数加以校正。这种经典的地基沉降计算方法通常假定土体受压时侧向完全限制,压缩性参数由一维压缩试验确定,与工程实际不符合。1考虑三向变形的沉降计算方法是由黄文熙所提出。他考虑了实际土体三向受力与三向变形条件,建议用三轴实测土的应力应变关系。因此,本方法是一种计及应力水平与应力路径影响的计算方法。
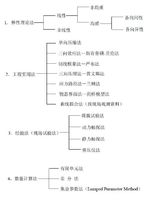
计算方法综述现行的土的地基沉降的计算方法有很多,可归纳为以下四大类(如图1所示):
第 1 类弹性理论法是将土体视为弹性体。测定其弹性常数。再用弹性理论计算土体中的应力与土的变形量。虽然在某些符合弹性理论基本假设的理想条件下可以采用,对于一般地基,由于土的压缩特性随处变化,边界条件比较复杂。加之用它不能求得土体变形随时间的变化,这类方法较少应用。
第 2 类的工程实用法是应用最多的方法。尤其是前面的两种。这类方法是按弹性理论计算土体中的应力,借试验提供各项变形参数,结合分层叠加原理,可以方便地考虑到土层的非均质、应力应变关系的非线性以及地下水位变动等实际存在的复杂因素。拟合法是利用现场已经测到的初期沉降资料,绘制沉降过程曲线,预估后期沉降量的方法。因依据的是实测资料,故计算结果有较高的可信度。
第 3 类经验法大多是采用现场测试结果,借经验相关关系,求得土的压缩性指标,再代入理论公式求解。对于无粘性土(如砂土等)取原状样进行室内试验有困难的情况,它不失为一种可行的途径。
第 4 类方法以有限元法为主。它实际上不能算是独立的一类。因为它只是利用计算机作为运算手段,还是以其它理论(主要是弹性理论)为依据,借有限单元法离散化特点,可计算复杂的几何与边界条件、施工与加荷过程、土的应力应变关系的非线性(包括各种本构关系)——以及应力状态进入塑性阶段等情况。尽管如此,成果的可信性归根结底还取决于输入指标的正确性与所用模型的代表性。这些还是值得进一步研究底课题。\
公式推导三向变形条件下的固结沉降计算法系由黄文熙所提出。本方法考虑了实际土体三向受力与三向变形条件,用三轴实测土的应力和应变关系。因此,本法是一种计及应力水平与应力路径影响的计算方法。
假设地基中一点由于基础荷重引起的附加正应力为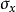 、
、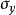 、
、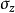 ,则该点的垂直应变见式:
,则该点的垂直应变见式:
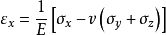
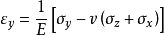
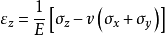
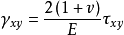
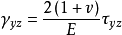
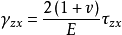
令,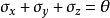 ,则有
,则有
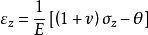
按弹性理论,由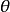 引起的单位体积变化应为:
引起的单位体积变化应为:
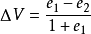
令上述二式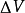 相等,故得:
相等,故得:
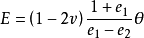
将上式代入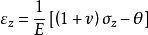 ,得:
,得:
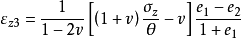
这就是三向应力状态下垂直应变的表达式。
对于平面应变问题,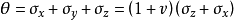 ,若令
,若令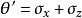 同样可得:
同样可得:
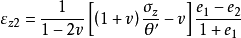
而地基沉降为:
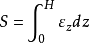
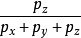 式
式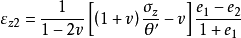 和
和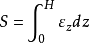 中的
中的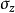 、
、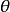 或
或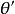 可以按弹性理论计算。v与e可在三轴试验中模拟土体在地基中的实际受力状态测定:v应视为
可以按弹性理论计算。v与e可在三轴试验中模拟土体在地基中的实际受力状态测定:v应视为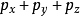 和
和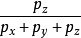 的函数。其中p为某点自重应力和附加应力之和。以此类似,可通过试验,找出一定的
的函数。其中p为某点自重应力和附加应力之和。以此类似,可通过试验,找出一定的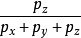 下,孔隙比e与
下,孔隙比e与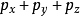 之间的关系。2
之间的关系。2
本词条内容贡献者为:
李勇 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国