[科普中国]-斯肯普顿极限承载力公式

浅基础的地基极限承载力是指使得地基达到完全剪切破坏时的最小压力，也就是相应于P~S曲线中地基从塑性变形阶段转为整体剪切破坏的界限荷载。斯肯普顿极限承载力公式是A.W.斯肯普顿提出的地基极限承载力公式，是一个适合于饱和软土地基上浅基础的地基极限承载力的半径验公式。

简介斯肯普顿极限承载力公式是由斯肯普顿提出的，对于不排水条件下的饱和粘性土，内摩擦角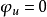 ，根据理论推导，条形荷载下的地基极限承载力 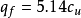，式中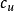 为地基土的不排水抗剪强度，考虑到基础形状和基础埋深的影响，对于基础埋深小于和等于2.5倍基础宽度的浅基础，建议按下式估算地基极限承载力

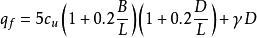式中L、B分别为基础的长边和短边；D为基础的埋置深度；γ为土的重度。

地基极限承载力地基极限承载力是指地基剪切破坏即将失稳时所能承受的荷载，它相当于地基上中应力状态从剪切阶段过渡到隆起阶段时界限荷载。随着荷载的增大，地基变形逐渐増大，初始阶段地基土中应力处在弹性平衡状态，具有安全承载能力。当荷载增大到地基中开始出现某点或小区域内各点在其某一方向平面上的剪应力达到土的抗剪强度时，该点或小区域内各点就发生剪切破坏而处在极限平衡状态，土中应力将发生重分布。这种小范围的剪切破坏区，称为塑性区。地基小范围的极限平衡状态大都可以恢复到弹性平衡状态，地基尚能趋于稳定，仍具有安全的承载能力。但此时地基变形稍大，必须验算变形的计算值不允许起过允许值。当荷载继续增大，地基出现较大范围的塑性区时，将显示地基承载力不足而失去稳定，此时地基达到极限承载力。随着对地基土破坏模式的认识的不断加深，地基极限承载力的理论公式也在不断完善，但大都是根据整体剪切破坏模式推导得出。极限承载力的求解方法有两种：一种是按照极限平衡理论求解，假定地基土是刚塑性体，当应力小于土体屈服应力时，土体不产生变形，如同刚体一样；当达到屈服应力时，塑性变形不断增加，直至土样发生破坏。这类方法是通过在土体中任取一微分体，以—点的静力平巧条件满足极限平衡条件建立微分方程，计算地基土中各点达到极限平衡时的应力和滑动面方向，由此求解地基的极限荷载。另一类是按照假定滑动面求解，通过基础模型试验，研究地基整体剪切破坏模式的滑动面形状，并简化为假定滑动面，根据滑动土体的静力平衡条件求解极限承载力1。

浅基础浅基础是指浅层地基所承载的基础。通常指其埋置深度不过5m，用普通开挖基坑的方法建造的基础。施工简便，可以用敞坑法施工，能直接观察基础底面地质情况。结构形式有：独立基础、条形基础、筏式基础和箱形基础等。常用于中小型建筑。用于浅基础的地基极限承载力计算的理论主要有普朗德尔极限承载力理论、太沙基承载力理论、魏锡克极限承载力公式等。这些理论的基本出发点都是按整体剪切破坏模式，在条形荷载作用下，假设滑裂面，由静力平衡条件推导出浅基础的地基极限承载力的表达式。在假设滑裂面、形成计算模式过程中，这些理论都对实际复杂的地基问题作出了不少相应的假设、简化。

普朗德尔极限承载力理论是1920年L.普朗德尔根据塑性理论，研究了刚性冲模压入模压入无质量的半无线体刚塑性介质时，导出了介质达到破坏时的滑动面形状和极限压应力公式。普朗德尔所做出的最主要的假设有：第一，土体是无质量的，即γ=0；第二，基底是光滑的，第三，假设所受的条形荷载是无限长的；第四，假设基础无埋深2。

太沙基承载力理论是由K·太沙基假设基底粗糙并考虑土自重影响导出的地基极限承载力理论。1943年提出，1967 年作了局部修改该理论将普朗德尔承载力理论应用到地基极限承载力课题。推导过程中做如下假设(1)受铅直均布荷载作用的条形基础，基底粗糙，不光滑；(2)条形基础浅埋；(3)地基土均匀、有重量，并考虑地基土自重对极限承载力的影响；(4)当荷载达到极限值时，地基发生整体剪切破坏。

魏锡克极限承载力公式是由A.S.魏锡克于20世纪70年代提出的地基极限承载力公式。在普朗德尔承载力理论基础上，考虑了土自重，并考虑了超载土的抗剪强度、荷载倾斜和偏心、基底倾斜、地面倾斜等因素对地基极限承载力的影响。魏锡克还提出可以判别地基三种剪切破坏型式的刚度指标和临界刚度指标，在地基极限承载力公式中列入压缩影响系数，以考虑局部剪切破坏或冲剪破坏时土压缩变形的影响。

本词条内容贡献者为:

耿彩芳 - 副教授 - 中国矿业大学