[科普中国]-应力条纹值

工程材料随着承受载荷的增大，材料在外力的作用下发生宏观变形时, 其内部分子间以及分子内各原子间的相对位置和距离发生变化, 产生的原子间及分子之间附加的内力, 抵抗着外力, 并力图恢复到变化前的状态;这种微观的分子运动, 宏观就表现为材料的应变,材料的光学性能也随之变化, 当二者达到平衡时, 附加内力与外力大小相等, 方向相反, 此时应变量达到最大, 在这过程中不断变化的应力条纹称之应力条纹值。

PC 材料的应力条纹值根据Tardy 补偿法的原理，对透明件用聚碳酸酯(PC)板材进行热光曲线实验，在不同加载状态下对条纹级次的变化进行了分析。结果表明：PC 材料仅需要较小的载荷即可出现理想的条纹级次；PC 材料受力后的应力响应时间对条纹级次有很大的影响；挤出成型获得的PC 材料具有惟一的加载方向以获得规则的条纹图。同时, 本研究获得了PC 材料的条纹值这一重要基础数据。

1 实验材料及设备

Lex an9034 聚碳酸酯板材(美国G E 公司生产)。试样厚度9mm , 直径40mm 。采用R409-2 型光弹仪，光源为钠光源。热光曲线实验使用烘箱。

2 实验方法

(1)热光曲线实验：选择载荷与升温方式，测定试样在圆偏振光场中的条纹级次。

(2)条纹级次的读取方法：采用对径受压圆盘理论模型，获得在不同的温度下材料受载后的中心点条纹级次， 非整数级条纹级次则采用Tardy 补偿法进行读数。具体步骤如下：

1)将光路系统设置为正交圆偏振光场，并使起偏镜和检偏镜的光轴分别与被测点的两个应力主轴方向一致，1/4 波片的快轴和慢轴与偏振镜光轴的相对位置保持不变；

2)确定被测点条纹级数所处的范围n 和n +1 ；

3)单独旋转检偏镜，观察等差线的移动。如果与被测点相邻的n 级整数级等差线移向被测点，当其刚好与该点重合时，记下检偏镜的旋转角度θ1，按式(1)计算被测点的条纹级数；如果与被测点相邻的n +1 级条纹移动到被测点，而相应的偏振镜转角为θ2，则按式(2)计算被测点的条纹级数。

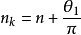(1)

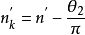(2)

(3)条纹值计算：

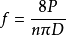(3)

式中：P 为载荷；D 为圆盘直径；n 为圆盘中心点条纹级次；nk 为被测点条纹级次。

3 实验结果

（1）载荷的选取对条纹级次的影响

实验以20N 为单位载荷递增选取了四组载荷，温度分别选取了常温、110 , 150 , 160 ℃四点对条纹进行了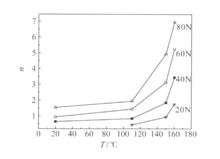观察, 实验结果见图1 。

（2）应力响应时间对条纹级次的影响

聚碳酸酯是典型的非结晶高聚物，当受到外力作用时，它达到对应的应变量需要一定的时间。选取载荷40N , 实验温度150 ℃，观察记录不同实验时间的条纹图，结果如图2 所示。

（3）加载方向对条纹图的影响

PC 沿任意方向加载，条纹图具有很强的方向性，图3 为加载方向与标定径向夹角分别为22 .5 ， 45，67.5 ，90°时加载的PC 材料条纹图1。

材料条纹值测定Sampson的正交异性光弹性定律为2

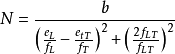( 4)

光弹性复合材料的3个独立的材料条纹值分别为

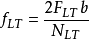
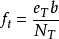
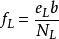( 5)

其中, f L、f T 及f LT应由单向应力状态确定。式中，eL 和eT 分别为纤维方向L 和垂直纤维方向T 的应力；fLT为“纯剪切”状态下的纯剪切应力，NL、N T、N LT为对应eL、eT 和fLT的等差条纹级数, b为模型厚度。按照前述应力分析，用E玻璃纤维和环氧树脂制成的单向纤维增强光弹性复合材料制成两根梁，一根梁轴线平行于材料纤维主方向L，另一根梁轴线垂直于材料纤维主方向L。两根梁的材料制备工艺，纤维含量，截面尺寸及跨度都是相同的。

测定材料条纹值f L、f T 时,按图1的方式分级加载，分别记录下两根梁在各级荷载作用下相应的等差条纹级次NL 和NT ，加载要使试件出现2～ 3级等差条纹。然后根据式( 5)中的前两式，即可求得正交异性光弹性的材料条纹值f L 和fT。测定另一材料条纹值f LT仍用上述两根梁,按图5的加载方式分级加载，记录下荷载大小及相应的等差条纹级次N LT ，根据式( 5)中的第3式，即可得到剪切条纹值fLT ，其值见表1。关于剪切材料条纹值测定的详细论述见文献3。

测定材料条纹值所用的试件, 是用含量15%的E玻璃纤维与环氧树脂制成的光弹性复合材料矩形截面梁,其跨度l= 140 mm，截面厚度b= 5 mm,截面高度h= 20 mm，测定f L 时荷载P= 720 N。试验测定是在409-Ⅱ 型光弹仪上进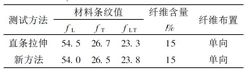行的。测出的材料条纹值结果见表4。

从表4可知,对纤维含量相同,制板工艺相同的光弹性复合材料,用不同的方法测定的f L、f T 及f LT具有明显的可比性,即测出的材料条纹值分别接近4。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学