[科普中国]-魏锡克极限承载力公式

简介

建筑物因地基问题引起的破坏，一般有两种可能：一种是由于建筑物基础在荷载作用下产生了过大的沉降差，致使建筑物严重下沉、上部结构开裂、倾斜而失去使用价值；另一种是由于建筑的荷载过大，超过了持力层上所能承受荷载的能力而使地基发生破坏。建筑物因承载力不足而引起的破坏，通常是由于基础下持力层土的剪切破坏所造成的。地基极限承载力的理论首先是由郎肯 ( Rankine W. J. M)于1857 年 提 出 的。 70 年代魏锡克 ( Vesic，A. S. )在前人的基础上，除了引入修正系数外，还考虑到地基土的压缩性的影响，把整体剪切破坏条件下的极限承载力公式推广应用于局部或冲剪破坏时承载力的计算。其形式如下：

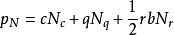
其中，c 为地基土的粘聚力，kPa；q 为地基两侧土的超载，kPa；r为地基土的重度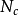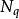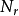；，，为承载力因数1。魏锡克地基承载力理论的基本假定为：刚塑体假定；土不可压缩；土体遵循莫尔一库仑强度理论；平面问题求解，维问题修正；基底完全光滑；地基土为均质单层土。普朗特尔和太沙基极限承载力公式都是在条形基础受中心竖直荷载并忽略基础两侧土的抗剪强度的影响的条件下得到的 。在工程实践中，经常可能遇到非条形基础 、 倾斜荷载或偏心荷载作用等情况。对于这些情况，一般都引入一些半经验的系数对承载力加以修正，即魏锡克极限承载力公式。魏锡克极限承载力公式计算粘性土的极限承载力结果与试验结果吻合较好，误差较小。

土的压缩性地基土在压力作用下体积缩小的特性称为土的压缩性。在一般压力作用下，土体的压缩变形主要是由于三个方面的原因：土颗粒发生相对移动，土中水及气体在外力的作用下从孔隙中排出，土颗粒和土中水被压缩。土颗粒和水被压缩与土体的总压缩量之比很小，基本可以忽略不计。土中水及气体从孔隙中排出是土体受压产生变形的重要原因，土的压缩变形的快慢与土中水向周边的渗透速度有关。对于饱和的无粘性土，由于透水性大，故在压力作用下土中水很快被排出，其压缩过程能很快完成；而饱和粘性土，则由于透水性较小，土中水的排出只能缓慢进行，故要达到压缩稳定需要相当长的时间。土颗粒发生相对移动的情况也是有的，但较排水固结来讲，相对量较小。土的压缩性高低以及压缩变形随时间的变化规律，可通过压缩试验或现场荷载试验确定。地基土在外力作用下（附加应力）所产生的压缩也可以通过经验公式来进行计算。现有计算理论有弹性理论法、分层总和计算法、应力面积法等。

地基极限承载力公式地基极限承载力是指地基土达到整体剪切破坏时的最小荷载。求极限荷载的方法有 两种：1.弹塑性理论求解法：根据弹性理论建立微分方程，并由边界条件求地基整体达 到极限平衡时的地基承载力精确解；2.假定滑动面法：假设滑动面形状（圆筒形、直线 形和直线与对数螺旋组合等），取滑动土体为隔离体，根据静力平衡求地基承载力。

普朗特尔地基极限承载力公式

普朗特尔（L.Prandtl，1920）研究的地基承载力课题：根据塑性理论研究一个刚性体，在外力作用下压入无限刚塑介质中，当介质达到极限平衡时，滑动面的形状和外荷载的计算公式。基本假设，朗特尔在推导极限承载力计算公式时做了如下三个基本假定：① 介质是无质量的；② 外荷载为无限长的条形荷载；③ 荷载板是光滑的，即荷载板与介质无摩擦。滑动面形状，朗特尔根据极限平衡理论及上述 3 个基本假定，得出滑动面的形状：两端为直线，中间为对数螺旋线，左右对称。

汉森公式

汉森在1970年提出的确定地基极限承载力公式。其基本假定和太沙基公式相似，但考虑了基础形状和埋深、荷载倾斜和偏心以及地面倾斜和基础底面倾斜等6个因素对极限承载力的影响，并用形状、深度、基底倾斜、荷载倾斜等修正系数和有效宽度的方法对太沙基极限承载力公式中的相应项逐一进行修正。适用条件：（1）倾斜荷载作用 汉森公式最主要的特点是适用于倾斜荷载作用，这是太沙基公式无法解决的问题。（2）基础形状 汉森公式考虑了基础宽度与长度的比值、矩形基础和条形基础的影响。（3）基础埋深 汉森公式适用基础埋深小于基础底宽（即 d

太沙基极限承载力公式

太沙基在 1943 年提出条形基础的极限荷载计算公式，它是基于以下基本假设推导得到的：①假定基础底面是粗糙的，②条形基础受均布荷载作用。地基土发生滑动破坏时，滑动面的形状：两端为直线，中间用曲线连接，且左右对称，和普朗特尔极限承载力的滑动面相似可以分为三区，