[科普中国]-奇异摄动控制

奇异摄动理论自诞生以来在数学领域和控制领域中均取得了突破性进展，并随着控制理论的发展而不断完善。若摄动问题的解Ur(x)，当r趋向于0时，不存在关于变量x一致收敛的极限，则称为奇异摄动问题。

奇异摄动问题的类型很多，故有许多种解决各类问题的方法。奇异摄动问题作为应用数学领域的一个活跃分支，其最早的数值方法是差分方法和有限元法。然而，研究发现，在参数非常小的情况下，网络步长越小所获解的精度越高，但网络步长太小也易引起数值不稳定现象。另外，奇异摄动问题中出现的方程往往是非对称的，如果用通常的有限元方法求解，则不能得到正确结果。也就是说，以上常用的两种数值计算方法解决奇异摄动问题是不适用的。因此，研究人员近30年主要专注于研究适用处理奇异摄动问题的差分方法(如拟合差分法、加权差分法和非均匀网络差分法)和广义Galerkin方法(如迎风有限元法和指数型拟合有限元法)，其中，涉及到常微分方程的初值问题和边值问题以及偏微分方程的奇异摄动问题。

在控制领域，处理奇异摄动问题主要采用边界层校正法，多年来，奇异摄动理论与方法以其特殊的优点，得到了国内外学者的广泛关注，麻省理工学院、加州大学洛杉矶分校等许多国外研究机构针对机器人、过程控制系统等进行奇异摄动建模与控制研究。

线性奇异摄动系统连续时间线性奇异摄动系统1)非时延连续时间线性奇异摄动系统

非时延连续时间线性奇异摄动控制系统模型为

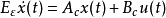
其中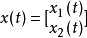， 为状态向量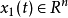， 为慢状态向量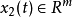， 为快状态向量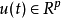， 为控制输入， 为摄动参数且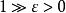 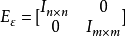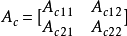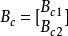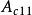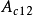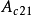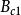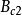， ， ， ， ， ， ， ， ， 为适当维数矩阵。

系统式的慢、快变分解成立的前提是 为非奇异，当 为奇异阵时，系统式不能直接进行慢、快分解。当 为非奇异时，称系统式为标准奇异摄动系统模型；而当 奇异时，则称系统式为非标准奇异摄动系统模型。
近年来，连续线性奇异摄动系统得到了充分的研究，其稳定性分析与控制研究可归纳为三种，即慢、快子系统分解方法，广义分解法以及整体建模与设计法。

(1)慢、快子系统分解方法。慢、快子系统分解的前提是系统式中的参数 为非奇异，因此该方法不能处理非标准连续线性奇异摄动系统。
(2)广义分解法。“广义分解法”从广义系统角度出发，将慢子系统描述为广义系统，从而克服“慢、快分解法”不能处理非标准连续线性奇异摄动系统的问题。对于充分小摄动参数，广义系统最优控制器的最优指标约等于奇异摄动系统的次优控制器的性能指标。基于Recursive方法可设汁高精度控制器¨列方法，分解Riccati方程法也可获得摄动参数无关的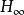 次优控制器存在条件。
(3)整体建模与设计法。经典的慢、快子系统分解法无法处理非标准线性奇异摄动系统。而广义系统方法的推导过程复杂，难以用线性矩阵不等式方法求解，学者们转而研究无需分解慢、快子系统的整体建模与设计法，基于极点配置的不确定性连续奇异摄动的动态输出反馈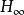 控制、具有Markovian跳变的线性奇异摄动系统状态反馈 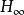控制等。

2)时延连续时间线性奇异摄动系统
具有常时延的连续时问线性奇异摄动控制系统模型为

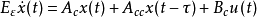
具有时变时延的连续时间线性奇异摄动控制系统模型为

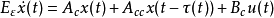
其中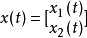， 为状态向量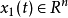， 为慢状态向量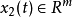， 为快状态向量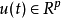， 为控制输入， 为摄动参数且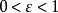 。 为时延常数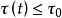， 为时变时延，且 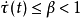。 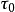与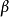 均为已知参数。 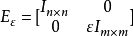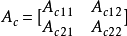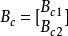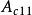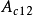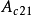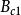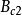， ， ， ， ， ， ， ， 为适当维数矩阵。
上式的慢、快变分解方法成立的前提是非奇异。当为奇异阵时，在上式形式下就不能直接进行慢、快分解。当非奇异时，称上式为标准时延连续时间线性奇异摄动系统模型；当奇异时，则称此系统为非标准时延连续时间线性奇异摄动系统。1

较之非时延连续线性奇异摄动系统，时延连续线性奇异摄动系统的研究并不多见。

离散时问线性奇异摄动系统与连续情形不同，由于采样速率的不同，离散时问线性奇异摄动系统模型存在多种表达形式。根据采样速率的慢、快程度，非时滞离散线性奇异摄动系统可分为标准离散线性奇异摄动系统和非标准离散线性奇异摄动系统，标准和非标准离散时间线性奇异摄动系统又分别存在两种形式。

标准离散线性奇异摄动系统模型一为

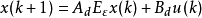
标准离散线性奇异摄动系统模型二为

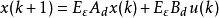
其中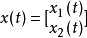， 为状态向量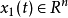， 为慢状态向量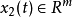， 为快状态向量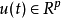， 为控制输入， 为摄动参数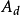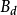，，为适当维数矩阵，。
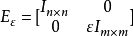非标准离散线性奇异摄动系统模型一为

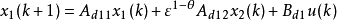
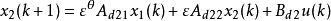
非标准离散线性奇异摄动系统模型二为

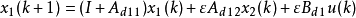
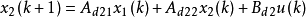
其中，。

①稳定性分析

非时延标准线性离散奇异摄动系统的研究处于初步阶段，其稳定性分析方法主要有频域法和时域法。频域法有Nyquist图法和Guardian映射多项式计算摄动参数稳定上界。时域法主要为基于临界稳定判据的摄动参数稳定上确界求解法。
②控制器设计
相对连续奇异摄动系统控制研究而言，离散奇异摄动系统控制问题的研究较少，基于Lyapunov函数的控制方法主要有：标准线性离散奇异摄动系统的调节器问题、基于LMI方法的鲁棒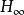状态反馈控制器设计、非标准线性离散奇异摄动系统的二次型调节以及观测器设计和保性能控制问题等。

经典非线性奇异摄动系统由于线性奇异摄动模型无法描述被控系统的非线性特性，学者们转而研究基于经典非线性奇异摄动模型的控制问题。针对非线性奇异摄动系统的稳定性分析问题，相继提出复合Lyapunov函数法、基于二次型Lyapunov函数的复合Lyapunov函数法以及向量Lyapunov函数法Ⅲ’等。在上述研究的基础上。进一步研究了系统参数存在不确定性的鲁棒稳定性及状态反馈控制问题、基于S-过程和LMI方法的系统受非线性时变摄动干扰下的二次可镇定性与非线性PI鲁棒镇定问题。基于经典非线性奇异摄动模型的早期控制方法主要为基于广义分解法的最优控制、Riccati方程法处理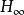控制问题以及基于区域极点配置的不确定性奇异摄动系统动态输出反馈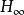控制，然而上述研究对性能指标的优化只是局部的。自80年代中期，积分流形法一度成为研究非线性奇异摄动系统控制的热点，但大都集中在快执行器驱动型系统，而且对系统结构的假设较多。1

总之，传统建模与控制法具有对系统结构假设多、推导过程复杂以及难以实现等缺点，研究成果多数限于仿射非线性奇异摄动系统。另外，研究主要集中于连续时间非线性奇异摄动系统的研究，针对离散时间情形的研究较少。

模糊奇异摄动系统
模糊奇异摄动建模与控制法是融合模糊逻辑理论与奇异摄动技术，研究非线性奇异摄动系统的分析与控制的方法，其核心思想是针对被控对象非线性奇异摄动系统，建立含有慢、快变量的模糊奇异摄动模型，从而设计摄动参数无关或有关的控制器。采用此类方法研究的非线性奇异摄动系统，统称为模糊奇异摄动系统。由于摄动参数的存在，模糊奇异摄动系统的分析与控制无法直接应用常规模糊系统理论与方法，否则将遇到摄动参数引起的数值求解中的病态问题。因此，模糊奇异摄动系统分析与控制方法成为研究热点。1

本词条内容贡献者为:

宋春霖 - 副教授 - 江南大学