[科普中国]-电磁场方程组

电磁场方程组由描述宏观电磁场现象普遍规律的方程式或方程组构成的。包括库仑定律，麦克斯韦方程组、静电场和恒定磁场的基本方程、无源区的波动方程等，揭示了不同条件下电磁场的普遍规律。

发展历史1819年，奥斯特发现了电流的磁作用，通过推理又导出了电流的磁化作用与电流之间的机械作用，实验结论是:运动电荷产生磁现象。

1820年安培发现磁铁对载流导体或载流线圈有作用力，从而得出了磁对运动电荷产生作用力的结论。至此，人们总结出磁现象与电荷的运动有密切的联系。

1831年法拉第经多年实验研究，于1831年发现了磁电感应产生的条件，这一重大发现在科学技术史上具有划时代的意义。法拉第发现了电磁感应现象，不仅揭示了电与磁相互联系和转化的重要条件，而且丰富了人类对电磁现象本质的认识，开拓了电能大规模利用、传输的道路，导致发电机的发明和人类电气时代的到来。法拉弟的研究方法主要是不断依靠实验，用实验来检验他的想法，在实验的直接影响下推动他的想法。

继法拉第电磁感应定律之后，安培在确立电流之间机械作用定律时所用的实验也是科学研究中最光辉的成就之一。他通过实验得出安培定律，而我们却看不出他的研究思想是怎样形成的。然而这些研究方法及成果仍就是麦克斯韦电磁场理论的数学方法的基础。

J.C.麦克斯韦提出了位移电流概念。电位移来源于电介质中的带电粒子在电场中受到电场力的作用。这些带电粒子虽然不能自由流动，但要发生原子尺度上的微小位移。麦克斯韦将这个名词推广到真空中的电场，并且认为：电位移随时间变化也要产生磁场，因而称一面积上电通量的时间变化率为位移电流，而电位移矢量D的时间导数（即дD/дt）为位移电流密度。它在安 培环路定律中，除传导电流之外补充了位移电流的作用，从而总结出完整的电磁方程组，即著名的麦克斯韦方程组，描述了电磁场的分布变化规律。

1845年，关于电磁现象的三个最基本的实验定律：库仑定律（1785年），毕奥-萨伐尔定律（1820年），法拉第定律（1831-1845年）已被总结出来，法拉第的“电力线”和“磁力线”概念已发展成“电磁场概念”。

1855年至1865年，麦克斯韦在全面地审视了库仑定律、毕奥—萨伐尔定律和法拉第定律的基础上，把数学分析方法带进了电磁学的研究领域，由此导致麦克斯韦电磁理论的诞生。

麦克斯韦电磁理论基础的电学和磁学的经验定律包括：静电学的库仑定律，涉及磁性的定律，关于电流的磁性的安培定律，法拉第电磁感应定律。麦克斯韦把这四个定律予以综合，导出麦克斯韦方程，该方程预言：变化的电磁场以波的形式向空间传播。 1865年麦克斯韦创立了普遍的电磁场方程组—麦克斯韦方程组,它是宏观电磁现象的基本规律 。

1887年德国物理学家赫兹 用实验证实了电磁波的存在。之后，人们又进行了许多实验，不仅证明光是一种电磁波，而且发现了更多形式的电磁波，它们的本质完全相同，只是波长和频率有很大的差别。按照波长或频率的顺序把这些电磁波排列起来，就是电磁波谱。如果把每个波段的频率由低至高依次排列的话，它们是工频电磁波、无线电波、微波、红外线、可见光、紫外线、X射线及r射线。

主要方程举例说明即便没有实物，占据空间的电磁场本身就具有能量、动量、角动量等传统实物的“物质”属性。充斥着电磁场的空间有能量、动量和角动量的存在。电磁场通过与实物的相互作用还能把能量、动量和角动量传递到实物中去。

自人们发现电现象、磁现象、电磁感应现象以来，对电、磁和电磁感应现象进行了深入广泛的研究，发现了电磁之间的关系及其规律，形成了完整、系统的电磁理论。电磁理论促进了科学技术的发展，有力的推动了社会的进步。电磁理论认为：变化着的电场伴随变化着的磁场，变化着的磁场也伴随变化着的电场。研究过程中通过方程的形式来描述电磁场基本规律就构成了电磁场方程组 。

库伦定律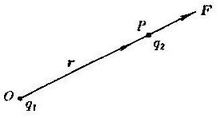库仑定律描述了真空中两个点电荷间相互作用力的规律。库仑定律的常见表述是：真空中两个静止的点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上，同名电荷相斥，异名电荷相吸。该定律由法国物理学家库仑于1785年在《电力定律》一论文中提出。库仑定律是电学发展史上的第一个定量规律，是电磁学和电磁场理论的基本定律之一。库仑定律没有解决电荷间相互作用力是如何传递的，甚至按照库仑定律的内容，库仑力不需要接触任何媒介，也不需要时间，而是直接从一个带电体作用到另一个带电体上的。

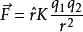
式中, K是比例常数，r是两点电荷间的距离，是从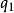 指向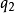 的单位矢量。若 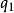和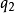 同号，该力是斥力，异号时为吸力。

库仑定律是在无限大的均匀、线性、各向同性介质中总结出的实验定律。静电力遵从叠加原理，当有多个点电荷存在时，其中任一个点电荷受到的静电力是其他各点电荷对其作用力的矢量叠加。对于连续分布的电荷系统（如体电荷、面电荷和线电荷），静电力的求解不能简单地使用库仑定律，必须进行矢量积分。

高斯定理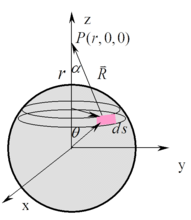

在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。高斯定律（Gauss' law）表明在闭合曲面内的电荷分布与产生的电场之间的关系。1电位移矢量在某一曲面上的面积分就是矢量通过该曲面的电通量，取积分曲面为半径为r的球面，电通量为 ：

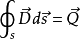此通量仅取决于点电荷量q， 而与所取球面的半径无关。 如果在封闭面内的电荷不止一个, 则利用叠加原理知, 穿出封闭面的电通量总和等于此面所包围的总电量。

毕奥-萨伐尔定律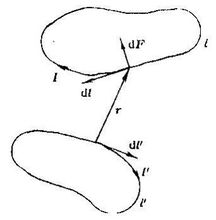毕奥-萨伐尔定律是由H.C.奥斯特实验（见电流磁效应）引起的，这个实验表明，长直载流导线对磁极的作用力是横向力。为了揭示电流对磁极作用力的普遍定量规律，J.B.毕奥和F.萨伐尔认为电流元对磁极的作用力也应垂直于电流元与磁极构成的平面，即也是横向力。他们通过长直和弯折载流导线对磁极作用力的实验，得出了作用力与距离和弯折角的关系。在P.S.M.拉普拉斯的帮助下，经过适当的分析，得到了电流元对磁极作用力的规律。根据近距作用观点，它现在被理解为电流元产生磁场的规律。

毕奥-萨伐尔定律适用于计算一个稳定电流所产生的磁场。这电流是连续流过一条导线的电荷，电流量不随时间而改变，电荷不会在任意位置累积或消失。采用国际单位制，用方程表示，电流元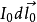 产生的磁感应强度为：

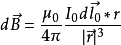
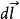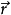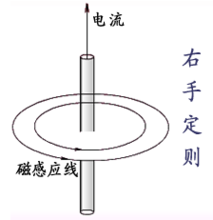
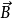，，三者满足右手螺旋关系。

积分通常围绕闭合曲线，因为电流只能在闭合路径周围流动。无限长的电线（如电流SI单位定义中所使用的安培）是一个反例。要应用公式，可以任意选择要计算磁场的空间点（r）。保持该点固定，计算电流路径上的线积分以找出该点处的总磁场。该法的应用隐含地依赖于磁场的叠加原理，即磁场是由电线的每个无穷小部分单独产生的场的向量和的事实。

安培环路定律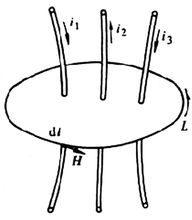在稳恒磁场中，磁感应强度B沿任何闭合路径的线积分，等于这闭合路径所包围的各个电流的代数和乘以磁导率，这个结论称为安培环路定理。安培环路定理可以由毕奥－萨伐尔定律导出。它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。

按照安培环路定理 ，环路所包围电流之正负应服从右手螺旋法则，在恒定磁场中，磁场强度矢量沿任意闭合路径l的环量等于其与回路交链的电流之和2，即：

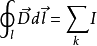
利用安培环路定理求磁场的前提条件：如果在某个载流导体的稳恒磁场中，可以找到一条闭合环路l，该环路上的磁感强度B大小处处相等，B的方向和环路的绕行方向也处处同向，这样利用安培环路定理求磁感强度B的问题，就转化为求环路长度，以及求环路所包围的电流代数和的问题，即利用安培环路定理求磁场的适用范围：在磁场中能否找到上述的环路，取决于该磁场分布的对称性，而磁场分布的对称性又来源于电流分布的对称性。

麦克斯韦方程组麦克斯韦方程组是电磁场方程组的基本方程组。麦克斯韦综合了静电学的库仑定律，涉及磁性的定律，关于电流的磁性的安培定律，法拉第电磁感应定律四个定理导出麦克斯韦方程，创立了普遍的电磁场方程组—麦克斯韦方程组,它是宏观电磁现象的基本规律 。

克斯韦方程组乃是由四个方程共同组成的：

高斯定律：该定律描述电场与空间中电荷分布的关系。电场线开始于正电荷，终止于负电荷。计算穿过某给定闭曲面的电场线数量，即其电通量，可以得知包含在这闭曲面内的总电荷。更详细地说，这定律描述穿过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。

高斯磁定律：该定律表明，磁单极子实际上并不存在。所以，没有孤立磁荷，磁场线没有初始点，也没有终止点。磁场线会形成循环或延伸至无穷远。换句话说，进入任何区域的磁场线，必需从那区域离开。以术语来说，通过任意闭曲面的磁通量等于零，或者，磁场是一个无源场。

法拉第感应定律：该定律描述时变磁场怎样感应出电场。电磁感应是制造许多发电机的理论基础。例如，一块旋转的条形磁铁会产生时变磁场，这又接下来会生成电场，使得邻近的闭合电路因而感应出电流。

麦克斯韦-安培定律：该定律阐明，磁场可以用两种方法生成：一种是靠传导电流（原本的安培定律），另一种是靠时变电场，或称位移电流（麦克斯韦修正项）。

方程组形式如下所示：

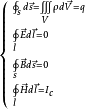
以上是麦克斯韦方程组积分形式，反映了空间某区域的电磁场量(D、E、B、H)和场源(电荷q、电流I)之间的关系。以自由电荷和自由电流为源头，而不直接计算出现于电介质的束缚电荷和出现于磁化物质的束缚电流和电极化电流所给出的贡献。由于在一般实际状况，能够直接控制的参数是自由电荷和自由电流，而束缚电荷、束缚电流和电极化电流是物质经过极化后产生的现象，采用这种表述会使得在介电质或磁化物质内各种物理计算更加简易。3

波动方程波动方程或称波方程（wave equations） 由麦克斯韦方程组导出的、描述电磁场波动特征的一组微分方程，是一种重要的偏微分方程，主要描述自然界中的各种的波动现象，包括横波和纵波，例如声波、光波和水波。波动方程抽象自声学，电磁学，和流体力学等领域。4

在无源区域中充满均匀、线性、各向同性的无耗媒质空间中，由麦克斯韦方程组，r=0，J=0可推出无源区电场波动方程

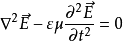
同理，可以推得无源区磁场波动方程为：

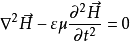
时变电磁场的电场场量和磁场场量在空间中是以波动形式变化的，因此称时变电磁场为电磁波。建立波动方程的意义：通过解波动方程，可以求出空间中电场场量和磁场场量的分布情况。但需要注意的是：只有少数特殊情况可以通过直接求解波动方程求解。

意义电磁学理论的发展在早期只是通过自然的语言描述电磁场中的一些规律。 法拉弟的研究方法主要是不断依靠实验，用实验来检验他的想法，在实验的直接影响下推动他的想法。由于他不是一个专业的数学家，他的研究成果没有用严谨的数学形式表示出来，只是用自然的、非技术的语言把这些事实表示出来。安培在确立电流之间机械作用定律时所用的实验也是科学研究中最光辉的成就之一。他通过实验得出安培定律，而我们却看不出他的研究思想是怎样形成的。

电磁学方程组着手从数学上阐述电和磁的理论，致力于解释法拉弟等物理学家对电磁学的研究成果。具有重要意义。 数学家的推理技巧使物理实验家看出他所测量出来的量是由一些必然的关系联系起来的。物理学家的发现向数学家揭示出一些形式新颖的量，那是数学家想象不出来的。物理学家用数学形式描述自然界的规律，赋予数学符号以明确的客观意义。5

数学家对数或量的符号进行某些脑力运算，并且从简单到复杂。这样我们能用不同的方式来表示同一事物，这些不同方式是等价的。数学家经过长期实践，已经成为将一种方式转化为另一种方式的专家，能够把令人困惑的表达转化为另一种可以用更易理解的语言来说明其意义的表达。
物理学研究总是不断揭示自然过程的新特征，因此我们总是在寻求适合这些新特征的新思想方式，重要的是仔细研究数学和物理学之间的关系。物理学研究人员观察不同情况下发生的各种现象，并力图推导出各种关系的规律。随着科学的发展，人们意识到要理解事物的过程及本质，首先应明确它属于哪一类，有多少种。这样数量质量被认为是科学探索中有待观察的主要特征。而且量的范畴也侵人到质的范畴，科学研究过程成为各种量的研究过程。研究人员把注意力集中到了认为是数量的那些现象的特征上，并寻找这些数量的内在联系，即物理学的研究也置于数学推理的影响之下。
数学家的推理技巧使物理实验家看出他所测量出来的量是由一些必然的关系联系起来的。物理学家的发现向数学家揭示出一些形式新颖的量，那是数学家想象不出来的。物理学家用数学形式描述自然界的规律，赋予数学符号以明确的客观意义。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学