[科普中国]-L1自适应控制

L1自适应背景

L1自适应控制算法是一种快速鲁棒的自适应控制。该算法实际上是模型参考自适应控制进行了改进，通过在控制律设计环节添加了一个低通滤波器，保证了控制律和自适应律设计的分离。

L1自适应系统机构L1自适应控制系统可分为：被控对象、状态预测器、自适应律、控制律

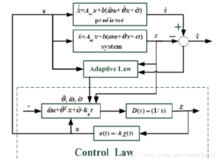
被控对象：采用状态空间形式表达，其中w、θ等为参数不确定性

状态预测器：数学模型如上图所示，其中x，w等对应的是被控对象当中的估计值。当时间趋于无穷时，被控对象将与状态预测器具有一致的动力学特性，估计偏差在李雅普诺夫意义下稳定

自适应律：以状态预测器和被控对象之间的误差为主要输入，保证其在李雅普诺夫意义下稳定而得到了对不确定性参数的估计

控制律：包括两个部分

1、与状态预测器相匹配的对参考输入的重构；

2、低通滤波环节。1

自适应控制理论简介自适应控制的研究对象是具有一定程度不确定性的系统，这里所谓的“不确定性”是指描述被控对象及其环境的数学模型不是完全确定的，其中包含一些未知因素和随机因素。

任何一个实际系统都具有不同程度的不确定性，这些不确定性有时突出在系统内部，有时突出在系统的外部。从系统内部来讲，描述被控对象的数学模型的结构和参数，设计者事先并不一定能准确知道。作为外部环境对系统的影响，可以等效地用许多扰动来表示。这些扰动通常是不可预测的。此外，还有一些测量时产生的不确定因素进入系统。面对这些客观存在的各式各样的不确定性，如何设计适当的控制作用，使得某一指定的性能指标达到并保持最优或者近似最优，这就是自适应控制所要研究解决的问题。

自适应控制和常规的反馈控制和最优控制一样，也是一种基于数学模型的控制方法，所不同的只是自适应控制所依据的关于模型和扰动的先验知识比较少，需要在系统的运行过程中去不断提取有关模型的信息，使模型逐步完善。具体地说，可以依据对象的输入输出数据，不断地辨识模型参数，这个过程称为系统的在线辩识。随着生产过程的不断进行，通过在线辩识，模型会变得越来越准确，越来越接近于实际。既然模型在不断的改进，显然，基于这种模型综合出来的控制作用也将随之不断的改进。在这个意义下，控制系统具有一定的适应能力。比如说，当系统在设计阶段，由于对象特性的初始信息比较缺乏，系统在刚开始投入运行时可能性能不理想，但是只要经过一段时间的运行，通过在线辩识和控制以后，控制系统逐渐适应，最终将自身调整到一个满意的工作状态。再比如某些控制对象，其特性可能在运行过程中要发生较大的变化，但通过在线辩识和改变控制器参数，系统也能逐渐适应。

常规的反馈控制系统对于系统内部特性的变化和外部扰动的影响都具有一定的抑制能力，但是由于控制器参数是固定的，所以当系统内部特性变化或者外部扰动的变化幅度很大时，系统的性能常常会大幅度下降，甚至是不稳定。所以对那些对象特性或扰动特性变化范围很大，同时又要求经常保持高性能指标的一类系统，采取自适应控制是合适的。但是同时也应当指出，自适应控制比常规反馈控制要复杂的多，成本也高的多，因此只是在用常规反馈达不到所期望的性能时，才会考虑采用。2

状态预测器含有参数不确定参数的被控对象数学模型可建立为：

x˙=Ax+Bu+σ′

其中A,B,σ表示系统的不确定性，其中A表示被控对象本身结构的不确定性，B表示输入引起的不确定性，而σ表示系统存在的扰动，与模型参考自适应控制系统设计类似

将被控对象转换为控制系统的期望输出表达
数学描述为：

x˙=Ax+Bu+σ′

其中Am满足霍尔维茨条件即满足稳定条件，r′=wu+θx+σ
对应可知，A=Am+bθ，B=bw，σ=bσ′

状态预测器设计
状态预测器是为了被控对象的不确定参数进行估计，其与被控对象具有一致的数学表达。则状态预测器建模为：

x^˙=Amx^+b(w^u+θ^x+σ^)

将被控对象与状态预测器相减可得，由参考输入$u$到误差$\tilde{x}$的状态表达式为：

x~˙=Amx~+b(w~u+θ~x+σ~)

为了保证上式是渐进稳定的，写出误差方程的能量函数：

V=12x~TPx~+12Γ−1(w~Tw~+θ~Tθ~+σ~Tσ~)

其中Γ为系统的自适应增益，对上式求导，写出能量函数导数。则可证明误差方程在李雅普诺夫意义下稳定。 1

自适应律设计自适应律设计部分，通过对估计参数确定其数学表达，保证误差方程在李雅普诺夫意义稳定，即对李雅普诺夫导数为负定。

w^=−Γ∫u(Pb)Tx~dt

θ^=−Γ∫x(Pb)Tx~dt

σ^=−Γ∫(Pb)Tx~dt

上式为自适应律部分，其为对不确定参数的估计，并保证了误差方程在李雅普诺夫意义下稳定

控制律设计对控制系统进行控制律设计，控制律环节输入为u`，输出为r的数学表达，其保证了输入到状态预测器输出是无稳定误差的（即输出可稳定的跟踪输入信号）：

状态预测方程（输入到输出的传递函数）为：

y~=c(sI−Am)−1b(w~u+θ~x+σ~)

当时间趋于无穷时，可达到：

y~=−cA−1mb(w^u+θ^x+σ^)

为保证y^=r则可得：

u=1w^(−1cA−1mbr−θ^x−σ^)

设计低通滤波器，并用L1小增益定理证明稳定性

设计低通滤波器D(s)=1s,对低通滤波器带宽k设计，为保证闭环控制系统满足L1小增益定理。

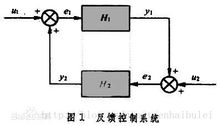
小增益定理：反馈系统中，u1 u2为系统的输入；y1 y2为系统的输出； e1 e2为误差信号；H1 H2为系统本身的特性。当H1 H2的L1范数增益乘积小于1时，系统满足内稳定条件

控制性能分析控制律设计保证了输入到y^的稳定性，需要分析输入到系统输出的稳态性能

结论：系统误差的L无穷范数的平方与控制系统自适应参数成反比，当自适应参数足够大时，系统误差在任意时刻趋近于0。