[科普中国]-体积锁死

概念

体积锁死，是有限元分析过程中经常出现的一种数值问题，一般发生在完全积分单元中。体积锁死是指完全积分单元受到过度约束时的一种锁死现象，如果材料是不可压缩的或是近似不可压缩的，完全积分单元可能会变得特别刚硬而不会产生体积变形，即所谓的“体积锁死“。

体积锁死的一个显著特征是：各个积分点之间或各个单元之间的静水压应力出现急剧变化。在可视化界面中绘制静水压应力的云纹图，如果看到静水压应力从一个积分点到另一个积分点的变化很大，呈棋盘形分布，就有可能出现了体积锁死的数值计算问题。1

产生原因本构方程给出了固体材料的应力和应变之间的关系，通常称为虎克定律。对于一般的各向异性材料，广义虎克定律可以用矩阵形式表示为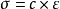，式中， 是材料常数矩阵，通常通过试验的方法获得。本构方程可以显式地写出，如图所示。应注意：由于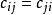 ，对于完全的各向异性材料总共有21个相互独立的材料常数 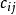；然而对于各项同性材料， 可以简化成如图所示。

式中，；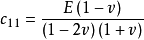

；

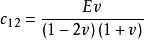上式中 分别是材料的杨氏模量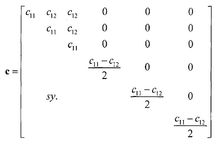，泊松比和剪切模量，这三个常数中只有两个是独立的。他们之间的关系是。

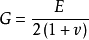由此可以注意到，当模型材料不可压缩或几乎不可压缩，泊松比接近于0.5，分母上的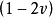 项趋于无穷小，从而使 趋于无穷大，若采用全积分运算即会产生体积锁定问题，即体积不变，体积模量太大，刚度太刚。2

解决办法选取适当的单元类型对于不可压缩材料的有限元分析，当塑性应变与弹性应变在同一数量级上时，二次完全积分单元容易出现体积锁死现象，往往还伴随着沙漏模式的数值问题，因此不能用于弹塑性分析中。如果必须采用完全积分的二次实体单元，则需要选择这种单元类型的杂交单元形式，但其计算费用大大增加。

如果使用二次减缩积分单元，当应变大于20%-40%时，需要划分足够密的网格才不会产生体积锁死。

建议使用的单元类型为非协调单元、线性减缩积分单元或修正的二次四面体单元。

细化网格在塑性应变较大的区域应划分足够细化的网格。

引入少量的可压缩性对于不可压缩材料，适当引入少量的可压缩性可以减轻体积锁死的现象。几乎不可压缩材料和完全不可压缩材料的计算结果很接近，因此可以将不可压缩材料的泊松比取为0.475-0.5之间的数值。