[科普中国]-粒度分离

粒度分离是利用孔径不同的筛子，将砂样分成粒径不同分级，又称筛分。

筛分的目的，一方面是有利于鉴定矿物，确定矿物的含量，也为了机械分离时，保证分离质量及效率；另一方面，根据矿物粒度的变化情况，可以提供物质沉积规律，搬运距离及方向，亦可提供有用矿物的可选性，为选矿加工提供资料。

粒度分离简介粒度分离在选矿厂很常见，通常包括筛分作业和分级作业两大类。

筛分所谓筛分，就是使松散物料通过单层或多层筛面分成多个不同粒度级别的过程，它是利用筛分机械（筛子）的筛面进行粒度分离。按照筛面的运动特性及筛面的形状可将筛子分为很多种，常见的有：

（1）固定筛。如固定棒条筛、固定细筛、弧形筛等。

（2）运动筛。如摇动筛、直线振动筛、旋转筛等。

筛分是利用筛面比较严格地按颗粒的几何尺寸进行粒度分离，因此分离的精度高。

筛分作业的目的就是分出入筛物料中粒度比筛孔尺寸小的那部分细粒级别。理想的情况是，粒度比筛孔尺寸小的所有颗粒都进入筛下物中，粒度比筛孔尺寸大的所有颗粒都留在筛面上形成筛上物。然而在实际生产中，由于多种因素的影响，筛上物中总是或多或少地残留～些粒度比筛孔尺寸小的细颗粒，而筛下物中有时也会因筛面磨损或操作不当混入一些粒度比筛孔尺寸大的粗颗粒。为了描述筛分作业完成的不完善程度，在实际工作中引入了筛分效率的概念。

所谓筛分效率，就是通过筛分实际得到的细粒级别的质量占入筛物料中所含的粒度小于筛孔尺寸的那部分物料的质量百分数。如果用QF、QP、Q筛上和α、β、θ分别代表人筛物料、筛下物、筛上物的质量和入筛物料、筛下物、筛上物中粒度小于筛孔尺寸的那部分物料的质量分数，则根据定义，筛分效率E的计算式为：

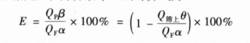
在实际生产中，由于直接测定QF和QP比较困难，所以常常根据筛分过程中物料量的平衡关系进行间接测定和计算筛分效率。

在物料的筛分过程中，存在如下的物料量平衡关系：

QF=Q筛上+QP

QFα=Q筛上θ+QPβ

由上述两式可推导出

QP/QF=（α-θ）/（β-θ）

将上式代图式（1）得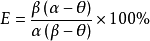 上述计算出来的筛分效率称为总筛分效率，即用小于筛孔的所有物料计算出来的筛分效率。

在研究筛分过程时发现，物料中筛下级别的粒级组成对筛分效率影响很大，细粒（易筛颗粒）容易透过筛孔，难筛颗粒很难透过筛孔，因而容易残存在筛面上。如果按各个粒级来计算筛分效率，则细粒部分的筛分效率要高些，而难筛颗粒的筛分效率要低些。因此，把按照筛下产品中某一级别物料的质量与入筛物料中同一级别物料的质量之比的百分数称为部分筛分效率。部分筛分效率计算公式同总筛分效率式，只不过此时α、β、θ的含义不是表示小于筛孔尺寸粒级的含量，而是表示要计算级别的物料的含量。

部分筛分效率与总筛分效率关系很大。细粒级的部分筛分效率总是大于总筛分效率，且级别愈细，部分筛分效率愈高；难筛颗粒的部分筛分效率总是小于总筛分效率，并且难筛颗粒尺寸愈接近筛孔尺寸，其部分筛分效率愈低。1

分级所谓分级，就是根据颗粒在流体介质中沉降速度的差异，将物料分成不同粒级的过程。按照所使用的介质，可分为风力分级（干式分级）和水力分级（湿式分级）两种；按照沉降方式，可分为重力沉降分级和离心力沉降分级。常用的分级设备有机械分级机、水力分级机、水力旋流器等。

由于分级是按颗粒的沉降速度差异实现分离，因此颗粒的尺寸、形状、密度及沉降条件等对其分离的精确性均有影响。

按沉降规律进行粒度分离的设备，计算其分级效率有许多标准，如量效率、质效率、总效率、修正效率、折算效率等。下面先介绍量效率、质效率和总效率的概念，至于修正效率和折算效率将在讨论水力旋流器数学模型时论述。

如下图所示，设分级给料、溢流、底流（或沉砂）的固体料量（t/h）分别为QF、QP、Q底，其中小于某粒度级别的产率分别为：α-χ、β-χ、θ-χ，则大于某级别的产率分别为α+χ=100-α-χ；β+χ=100-β-χ；θ+χ=100-θ-χ。

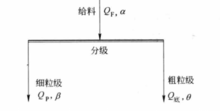
分级量效率。分级的目的是在指定的粒度下，使细、粗颗粒分别进入溢流和底流（或沉砂）。因此可以考虑两个方面，即细级别进入溢流和粗级别进入底流的回收率，二者愈高愈好，此二指标可分别用其量效率来评价。

细级别存溢流的回收率，即细级别存溢流的量效率E-χ为：

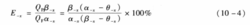
粗级别在底流中的回收率，即粗级别在底流中的量效率Eˊ+χ为：

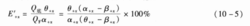
由式（10-4）很容易算出细颗粒在底流中的回收率Eˊ-χ=100一E-χ。；由式（10—5）很容易算出粗颗粒在溢流中的回收率E+χ=100一Eˊ+χ。很显然，细颗粒在溢流中的回收率高、粗颗粒在溢流中的回收率低时，分级设备的作业效率才真实反映出来，这就需要用分级质效率来计算。1

粒度分离的理论基础1.引言

应用筛分和分级对粉碎颗粒实现分离，筛分是按颗粒的大小和形状进行分离，分级则是按颗粒大小、形状和密度的差异进行分离；所以如此，是因为上述性质共同影响颗粒在流体介质中的运动。

2.使用水力分级的粒度分离

流体中的颗粒运动。颗粒在静止或流动的流体（液体、空气或气体）中沉降，大小、形状和比重不同的颗粒群被分离成性质更为均一的许多组份。由于不同物理性质的颗粒在介质中具有不同的移动速度，因此产生分离现象。在重力影响下，颗粒在液体中沉降，同时遇到一个阻力。当该阻力等于颗粒的有效重量时，颗粒达到恒定的最大沉降速度，通常称之为临界沉降速度。对球体而言，此临界速度（Vm）可由下式算出：

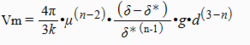
式中μ一流体的粘度；δ一固体的密度；δ*一流体的密度，g一重力加速度；d一球体的半径，n和k一颗粒半径的函数。可将思托克斯和牛顿定律看作是上图方程式的特例：
思托克斯定律：

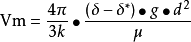
该定律是当n=l和k=6时，用于小固体颗粒（比如说半径达0.005厘米的石英球）在水中的降落，这时移动速度低且为层流或粘滞流动（即流线平滑且连续）。

牛顿定律：

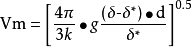
这个定律是当n=2和k=（π/2）**·**Q（Q为阻力系数）时，用于大固体颗粒（如石英颗粒的半径大于0.25厘米）在水中降落，这时移动速度高为紊流。环绕固体颗粒的液体流线型流动仅限于雷诺数Re=（Vmdδ/μ）小于1的条件，如果Re大于2000时，流动则为全紊流。在矿物处理中，最为适用的是层流和紊流之间的范围，但是这些条件的理论没有充分加以研究。

在理想情况下，可以利用上面三个方程来预测流体中颗粒的运动，并适当地加以修正以考虑某些因素，例如考虑：（1）颗粒的形状不规则；（2）其它颗粒干扰该颗粒的降落以及分离容器器壁影响颗粒的降落。

但在实践中，不能很准确地确定这些因素，而且所遇到的流动方式是如此复杂，以致这些方程不能用于工业回路的分析和模拟。因此必须使用另外的模拟方法。2

本词条内容贡献者为:

蒲富永 - 教授 - 西南大学