[科普中国]-环形等离子体

环形等离子体位形轴对称系统的磁面

在处理环形聚变等离子体平衡时，一般可采用磁流体模型。其平衡方程是

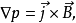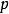其中 和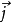 分别为动力压强和电流密度。在轴对称情形，用柱坐标将上式写成分量形式

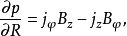
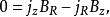
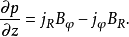从上面第二式可得到 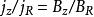，或者说在 （子午面内）电流与磁场的投影同向（或方向相反）。所以电流所在面与磁场所在面重合。但在这一面上，它们一般不重合，而有一夹角，使得满足上述平衡方程。从这一方程可知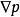， 垂直于这一面，所以 就是此面。这样的曲面称为磁面。根据一项 提出的定理，处处非零的向量场必然处在一环拓扑面上。在托卡马克位形中，磁面结构是套在一起的拓扑环面。其中最里面的退化为磁轴。由于磁面上的输运远远大于垂直于磁面的输运，一般磁面上的电子温度和电子密度也相等。

对于一个环拓扑但不是轴对称的系统如仿星器，也可定义电流和磁场所在的面为磁面。但是没有定理显示，一定处处存在磁面。

对于不存在电流的真空磁场，如在仿星器里，如果不存在等离子体，可以在一极向截面选择任意点，从这点出发沿磁力线多次绕环向返回这一截面所得交叉点的轨迹就是磁面。存在确定磁面的条件是存在极向磁场。一个纯环向场就没有确定的磁面。

磁通和磁面量准确描述磁面的物理量是极向磁通。它可理解为一个封闭环形磁面内的总的极向磁通量，定义为

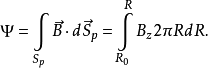曲面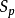 是一个环带，一侧为磁轴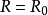（ ），另一侧在磁面上（图1）。前一式适用于环拓扑，后一式仅适用于轴对称。实际上，磁通可任意加减一个常量而不改变物理问题性质，所以我们可视方便令任意磁面上的磁通为零，也就是说上述积分从这个磁面开始。

用磁通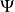 对磁面定量描述。我们说某物理量为磁面量时，与说它是 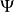的函数一个意义，如动力压强 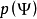。我们使用磁通的这个定义时，常常在公式中出现 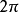。为简单起见，常使用另一磁通定义（约化磁通）

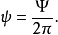
现在我们求极向磁通的全微分。考察两个距离非常近的磁面（图2），令一个的极向磁通为零，用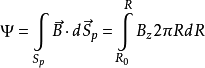 式子的第一个求另一个的磁通，实际上就是求两个磁面间的磁通。1

环形等离子体内的粒子运动热运动和漂移运动在环形磁场位形中，带电粒子做两种运动，即无随机的热运动和在电场下的漂移运动。我们假设等离子体的电子温度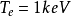 ，电子的平均热运动速度是

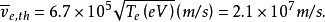我们假设等离子体的截面为 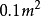，等离子体电流为 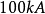。则电流密度 。再设电子密度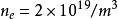 为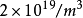 ，则电子漂移速度

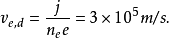一般来说，电子在电场中的漂移速度比其热运动速度小得多。所以我们首先可暂不考虑其漂移运动。

约束粒子和飞越粒子托卡马克有足够强的环向磁场，带电粒子满足绝热条件。环向磁场与大半径成反比分布，外弱内强。部分粒子从外侧向内侧运动时，就会被强磁场反射。它们在上下两个强场反射点间往返运动，不能达到环内侧。它们在环向也作往返运动，不能持续绕大环运动。这样的粒子称为约束粒子。当然也有一部分粒子能越过环内侧磁场最强点而环绕小截面也环绕大环在一个方向持续运动，称为飞越粒子。通过碰撞和其它作用，两种粒子可以相互转换。1