[科普中国]-n叉树- · 科普中国网

定义

二叉树中每个结点有一个数据项,最多有两个子节点,如果允许树的每个节点可以有两个以上的子节点,那么这个树就称为n阶的多叉树，或者称为n叉树。

性质

每个节点有m个子节点和m-1个键值。

每个节点中的键值按升序排列。

前i个子节点中的键值都小于地i个键值。

后m-1个子节点中的键值都大于第i个键值。1

分类

典型的n叉树有2-3-4-Tree和B-Tree两种。

B树

B树（B-tree）是有Bayer和McCreight在1972年提出的数据结构。B树索引是数据库中存取和查找文件(称为记录或键值)的一种方法，应用于磁盘读取方面。

B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同，B树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。

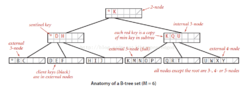
B树的一些性质

根据Knuth's的定义，n阶B树（a B-tree of order n）是具有以下性质：

每个点最多有n个孩子

每个非叶子节点（根节点除外）最多有n/2(向上取整)个孩子

root至少有2个子树，除非root的孩子是叶子节点

k个孩子的非叶子节点含有k-1个键值

所有的叶子节点都在同一层，并且内部节点不携带任何信息。（B树的阶指最大子节点数。优势，n阶的B树节点定义为有k个键值和k+1个指针，其中nnode->keyTally||node->keys[i-1]>K) return BTreeSearch(K,node->pointers[i-1]); else return node; } else return 0; } B树的插入

伪代码如下：

BTreeInsert(K) 找到一个叶节点node来插入k while（true）在数组keys中为k找到一个合适的位置； if node 不满插入K并递增keyTally； return； else 将node分解为node1(=node)与node2(新节点)；在node1和node2之间平均分配键值和指针，并正确地初始化他们的keyTally； k=中间键值 if node 是根节点穿件一个心的根节点，作为node1和node2的父节点将K及指针node1和node2的指针妨碍根节点中，并将根节点的keyTally设为1； return； else node = 其父节点。//处理父节点