[科普中国]-热力学特性函数-

热力学函数独立变量的选择有任意性。马休在 1869 年证明，如果适当选择独立变量（称为自然变量），只要知道一个热力学函数及它的自然（正则）变量，就可以通过求偏导而求得均匀系的全部热力学函数，从而把均匀系统的平衡性质完全确定，这个热力学函数即热力学特性函数。

热力学特性函数及性质在热力学中，最基本的是物态方程、内能和熵，其它热力学函数均可由这3个基本函数导出。由于处于平衡态的系统，其性质由热力学函数描述，因此，只要知道这3个基本热力学函数，均匀系统的平衡性质就完全确定了。也就是说，要确定均匀系统的平衡性质一般需要知道3个函数1。

如果由某一函数可导出上述3个基本热力学函数，这一函数就可以完全确定一个均匀系的平衡性质，表明它是表征均匀系统特性的，那么该函数就被称为这个系统的特性函数。如果特性函数存在，那么要确定均匀系统的平衡性质只需要知道一个函数就可以了。

例如，对于一个热力学函数若适当地选择其独立变量时，即U(S,V)，H(S,p)，F(T,V)，和C(T,p)就可以用其中任一个状态函数来导出3个基本热力学函数，从而推得体系所有其它的热力学函数（包括U,H,F,S,T,p,V等）。如此选定独立变量的热力学函数，因具有以上的特性，故为热力学特性函数2。

特性函数的应用证实特性函数的存在是热力学的重大成就．但由于这些函数的表达式不能从热力学定律本身得到，使得在热力学范围内，仍然没能充分利用这些成就。然而，由于特性函数本身所具有的性质——由它可以推得体系所有其它的热力学函数，即它可以直接和其它热力学函数（或它们的偏导数）联系起来，这就决定了应用它会给解决热力学问题带来极大的方便3。

在热力学中，涉及热力学函数偏导数的恒等式证明题很多，证题的技巧性也很强，但应用特性函数来求证就不需要更多的数学技巧。下面列举实例具体说明。

焓态方程：

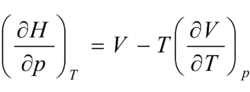
的导出。

观察欲证等式，变量为T,p，如果选择T,p为独立变量，C(T,p)为特性函数．由吉布斯函数和焓的定义式，可知 C 与 H 的关系为：

H=C+TS

则：

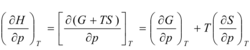
由热力学基本方程dC=-SdT+Vdp及麦氏关系，可得焓态方程：

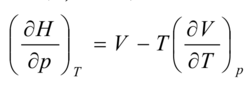
类似的证明问题在热力学中还有很多，通常的做法都要利用一些数学关系式，如偏微商的循环关系式和链式及倒置式、全微分式及其判别式、雅可比式等来解决，技巧也主要在证明的每一步选择什么公式进行变换能使证明最简单，可以说一题一法，较难掌握3。

本词条内容贡献者为:

蒲富永 - 教授 - 西南大学