[科普中国]-费曼路径积分

概念

费曼的路径积分理论与量子力学曲率解释在数学意义和物理意义上是完全吻合的。在量子力学曲率解释中不需要知识波的纠缠，曲率波是真实的物理波，它在时空中的干涉现象直接体现粒子在时空中的真实分布，波与粒子在物理意义上是完全统一的。

根据费曼路径积分对粒子宏观轨道的理解，在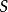 取极值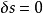 的那条轨道（由一系列的点组成）的邻域轨道，相位的贡献均使曲率波幅不是相消，而是相加，总曲率幅大大加强，给出与宏观粒子对应的明显的一条可视轨线（如图1）。

在这条轨线上，粒子所经的每一点都具有与轨线邻域外的点更大的曲率，而轨线邻域以外的点曲率幅相消得很厉害，空间变得很平坦。

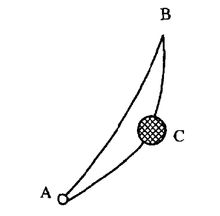
通过费曼路径积分的曲率波诠释，不但能更好地理解微观世界中的干涉现象，衍射现象也能得到自然的说明。例如，粒子从A到B，如在通路S旁有一障碍物C(如图2），由于C的遮挡作用，曲率波在B处的传播必然受到影响，因而到达B点的曲率波的总曲率波幅与C不存在时的情况就有所不同，表现出来的就是衍射现象。与量子现象相反，一个经典的粒子只走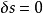 所规定的一条轨道，只要C不横亘在 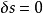的轨道上，就不会对粒子有影响，不会产生衍射现象。1

基本原理费曼路径积分的本质是基于假设波函数 代表粒子经过任意道路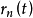 ，从A到B在B点的几率幅，且传播子

的平方

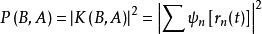代表粒子在B点被测到的几率。

在 式子中，

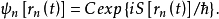
上式中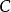，为归一化函数。

其中，

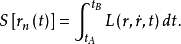
在量子力学曲率解释中，波函数代表粒子沿任意路径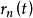从A到B点在B点的曲率波动，式子则代表所有路径到达B点曲率波的叠加。式子则代表粒子各条路径在B点形成的叠加态的平方，与总曲率成比例，它表示粒子在B点的可视程度，对应粒子在B点的可测几率。

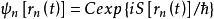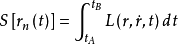、两个式子则表明，粒子从不同途径到达B点的曲率波振幅虽然相同，但相角却不同，因而每条路径传来的波对B点弯曲的贡献却不同。如果B点是变化的，则随着B点的变化，有些地方是曲率相加，有些地方是曲率相消，故会出现曲率波的干涉现象。实际干涉条纹中，明亮的地方曲率相加，暗的地方曲率相减，条纹的明暗表明曲率大小的变化。实际问题中，各种可能的道路是连续变化的，因而式变为

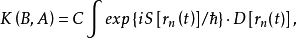上式中就是表示对给定初、终点的一切连续变化可能轨道积分。1