概念
如果我们设想由基态基本子构成的真空点阵是像氯化钠晶体那样的立方点阵,当做为阵点的基态基本子激发而使真空单胞变成粒子时,单胞的对称性也要发生变化。因为正如由原子或离子构成的晶体,当原子或离子的种类变化如原子或离子的体积变化时,也会引起晶体对称性的变化,甚至从一种晶系变为另一种晶系。基态基本子和激发态基本子不但质量-能量相差很大,体积的变化也应很大,因为这样微小的粒子的大小是可以用其德布罗意波长来估计的。由于德布罗意波长与粒子的能量关系如下:
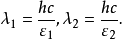 因此有两粒子的德布罗意波长比:
因此有两粒子的德布罗意波长比:
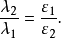
|| || 表1
如果用这个比值估计两个基本子大小的比值,则可从表1看到,基态基本子和激发态基本子的大小相差悬殊。
计算表1时,除了采用表1的数据外,还取基态基本子的能量分别为
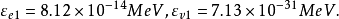
显而易见,构成真空单胞的基态基本子的激发,应引起真空单胞的某种变化,如单胞体积的变化、对称性的变化等。如果用晶体类比,构成晶体的原子或离子变化时,会司引起晶体点阵单胞的大小和对称性变化。
众所周知,在粒子物理中本来就有这样的类比:认为卡比坡角或温伯格(StevenWeinberg,1933~)角类似于晶体中的光学角度。例如,在高能中微子与夸克或核子的相互作用中,其散射截面因产物不同而与这两种角有不同的关系。其中,当产物中有带电荷的轻子时,散射截面都与卡比坡角的正弦平方或余弦平方有关:当产物中只有中微子时,散射截面则与温伯格角的正弦平方有关。
这些事实表明,如果把卡比坡角和温伯格角看成是真空单胞激发时对称性变化的一种表现,有如晶体光学角度的变化,那么,我们就可以更直观地讨论相应的问题。1
基本原理关于温伯格角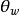 的物理意义,可以形象地说明如下:在格拉肖-温伯格-萨拉姆理论提出之前,电磁作用和弱作用的理论是分别独立的,其有关参量如表2所示。
的物理意义,可以形象地说明如下:在格拉肖-温伯格-萨拉姆理论提出之前,电磁作用和弱作用的理论是分别独立的,其有关参量如表2所示。
|| || 表2
表2中电磁作用耦合常数 和弱作用耦合常数
和弱作用耦合常数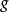 之间无联系。
之间无联系。
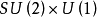 的弱、电统一理论认为,统一场的各个场量子
的弱、电统一理论认为,统一场的各个场量子 都处于同等的地位,都是此理论中的规范场的场量子,其参量和描述方式见表3。
都处于同等的地位,都是此理论中的规范场的场量子,其参量和描述方式见表3。
|| || 表3
描写弱、电统一的流是 和
和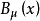 ,传递量子为
,传递量子为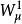 ,
,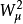 ,
,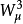 和
和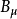 (可重新组合成
(可重新组合成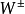 、
、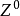 和
和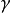 ),而弱电统一的耦合常数为
),而弱电统一的耦合常数为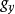 和
和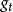 。
。
表2中的耦合常数 和
和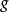 (可以直接测量)与表3中的耦合常数
(可以直接测量)与表3中的耦合常数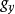 和
和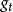 (不能直接测量)之间的关系可用图1表示。
(不能直接测量)之间的关系可用图1表示。
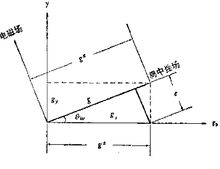
图1中以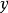 、
、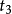 代表弱电统一理论的两个轴,基本耦合常数
代表弱电统一理论的两个轴,基本耦合常数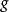 在
在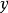 和
和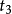 两轴上的投影分别为
两轴上的投影分别为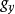 和
和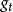 ,
,
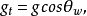
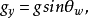
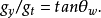
取弱中性耦合常数 ,弱带电耦合常数
,弱带电耦合常数 ,电磁场与弱中性场的一组轴和以
,电磁场与弱中性场的一组轴和以 、
、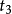 轴相对旋转角
轴相对旋转角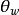 .由图4可知
.由图4可知 是
是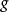 的二次投影,即
的二次投影,即
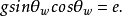 由图4及
由图4及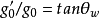 和
和 两个式子可知,
两个式子可知,
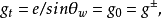
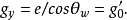
由此可见,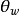 实际上是连续两类耦合常数的一个参量,也是连续弱作用和电磁作用耦合常数的一个参量。2
实际上是连续两类耦合常数的一个参量,也是连续弱作用和电磁作用耦合常数的一个参量。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国