概念
如果某种连续整体对称性是自发破缺的,则一定存在零质量的玻色子,即Goldstone玻色子。原来由复标量场描述的量子系统,当发生对称性自发破缺后就转化为实际量粒子和Goldstone玻色子构成的量子系统。当体系的连续对称性自发破缺时,会产生一种无能隙的无自旋玻色子(spinless boson)。声子就是一种goldstone玻色子,并且你会发现在其色散关系中,长波极限下能量为0。1
基本原理考虑经典复标量场的拉氏密度:
 其中
其中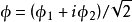 ,
,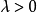 。
。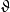 在连续相位变换(
在连续相位变换(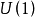 转动变换)
转动变换)
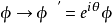 之下是不变的。拉氏密度
之下是不变的。拉氏密度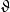 中的势能项为
中的势能项为
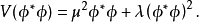 当
当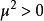 时,势能最低点对应于
时,势能最低点对应于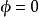 (真空态),即复平面
(真空态),即复平面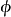 上的坐标原点,有严格的对称性。在
上的坐标原点,有严格的对称性。在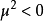 的情况下,可由
的情况下,可由
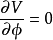 决定真空态的场:
决定真空态的场:
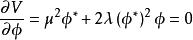 ,即
,即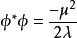 。另一方面,由
。另一方面,由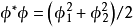 ,故得圆方程:
,故得圆方程:
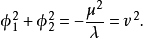 可见,这时的真空态是无限简并的,每一个真空态对应于
可见,这时的真空态是无限简并的,每一个真空态对应于 平面上半径为
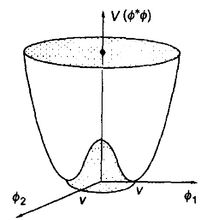
平面上半径为 的圆周(势能最低)上的一个点(图1)。
的圆周(势能最低)上的一个点(图1)。
各点之间的相互关系由相位变换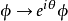 决定。像前例一样,选定一个真空态:
决定。像前例一样,选定一个真空态:
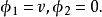 这个真空态在相位变换
这个真空态在相位变换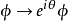 之下不再是不变的。因而在
之下不再是不变的。因而在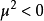 情况下,对称性是自发破缺的。
情况下,对称性是自发破缺的。
引入新的场量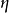 和
和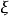 ,满足
,满足
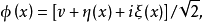 使得
使得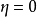 ,
,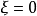 对应真空态。代入
对应真空态。代入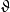 得:
得:
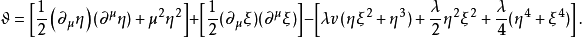 式中第一个方括号内是自由标量场拉氏密度式的形式,
式中第一个方括号内是自由标量场拉氏密度式的形式,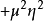 项说明
项说明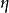 场对应于质量为
场对应于质量为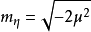 的粒子(
的粒子(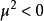 )。第二个方括号是粒子质量为
)。第二个方括号是粒子质量为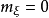 的自由标量场,称为Goldstone玻色子。第三个方括号是相互作用项。无质量玻色子的出现可通过图2的经典对应来说明。
的自由标量场,称为Goldstone玻色子。第三个方括号是相互作用项。无质量玻色子的出现可通过图2的经典对应来说明。

势能最小处位于谷底的圆周上。有质量的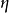 模式对应于有恢复力的“径向振荡”,通常说,
模式对应于有恢复力的“径向振荡”,通常说,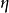 场自发地获得了它的质量;无质量的
场自发地获得了它的质量;无质量的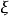 模式对应于谷底圆周上的无阻尼运动(无质量激发)。谷底圆周上的无数个点的整体具有严格的旋转对称性,但是现实的真空态只有一个,只能是其中一点.对于这一点(即现实的真空态)来说,原有的旋转对称性就不再保持了。这也就是对称性的自发破缺。1
模式对应于谷底圆周上的无阻尼运动(无质量激发)。谷底圆周上的无数个点的整体具有严格的旋转对称性,但是现实的真空态只有一个,只能是其中一点.对于这一点(即现实的真空态)来说,原有的旋转对称性就不再保持了。这也就是对称性的自发破缺。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国