定义
严格凹函数是定义在某个向量空间的凸子集C(区间)上的实值函数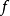 (x) ,而且对于凸子集C中任意两个向量p,q,
(x) ,而且对于凸子集C中任意两个向量p,q,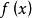 满足1
满足1
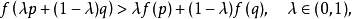 则称
则称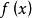 是定义在凸子集C中的严格凹函数。容易证明,其定义等价于若
是定义在凸子集C中的严格凹函数。容易证明,其定义等价于若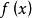 满足
满足
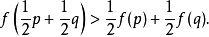 对任意两个向量p,q成立。特别地,若这里凸集C即某个区间 I ,那么就是:设
对任意两个向量p,q成立。特别地,若这里凸集C即某个区间 I ,那么就是:设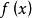 为定义在区间 I 上的函数,若对 I 上的任意两点
为定义在区间 I 上的函数,若对 I 上的任意两点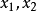 和
和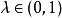 ,有1
,有1
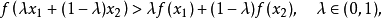 成立,则称
成立,则称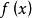 是定义在区间I 中的严格凹函数。
是定义在区间I 中的严格凹函数。
在上面的定义中,若将小于号改变小于等于,则上面的函数称之为凹函数。
判别方法引理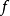 为 I上的凹函数的充要条件是:对于I的任意三点
为 I上的凹函数的充要条件是:对于I的任意三点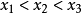 ,总有
,总有
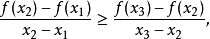 证明:
证明:
必要性:
设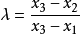 ,则有
,则有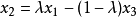 ,由凸性的定义代入,从而有
,由凸性的定义代入,从而有
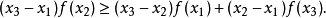 整理后即可得到。
整理后即可得到。
充分性:
在I上任取两点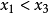 ,在
,在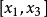 上任取一点
上任取一点 ,由必要性的推导逆过程,可证得
,由必要性的推导逆过程,可证得
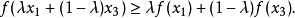 故为I上的凹函数。证毕。
故为I上的凹函数。证毕。
推论1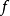 为 I上的函数,下列条件等价:
为 I上的函数,下列条件等价:
1)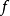 为 I上的凹函数的。
为 I上的凹函数的。
2)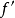 为I上的减函数。
为I上的减函数。
3) 对I上的任意两点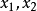 ,有
,有
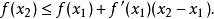
推论2对于实数集上的函数,如果其二阶导数在区间上非正,就为凹函数。如果其二阶导数在区间上恒小于0,就为严格凹函数1。
严格凹函数的性质1)一元可微函数在某个区间上是严格凹的,当且仅当它的导数在该区间上严格单调减的。
2)一元连续可微函数在区间上是严格凹的,当且仅当函数位于所有它的切线的下方:对于区间内的所有 和
和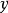 ,都有
,都有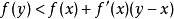 。特别地,如果
。特别地,如果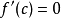 ,那么c是
,那么c是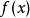 的最大值。
的最大值。
3)一元二阶可微的函数在区间上是严格凹的,当且仅当它的二阶导数是负的;这可以用来判断某个函数是不是严格凹函数,但反过来不成立。更一般地,多元二次可微的连续函数在凸集上是严格凹的,当且仅当它的黑塞矩阵在凸集的内部是严格负定的。
4)严格凹函数的任何极大值也是最大值。严格凹函数最多有一个最大值。
5)对于严格凹函数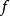 ,水平子集
,水平子集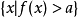 和
和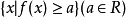 是严格凸集。
是严格凸集。
6)反向延森不等式2对严格凹函数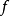 都成立。
都成立。
7)如果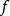 和
和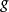 是严格凹函数,那么
是严格凹函数,那么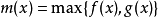 和
和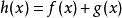 也是严格凹函数。
也是严格凹函数。
8)如果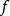 和
和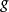 是严格凹函数,且g递减,那么
是严格凹函数,且g递减,那么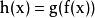 是严格凹函数。
是严格凹函数。
9) 凸性在仿射映射下不变:也就是说,如果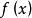 是凹函数,那么
是凹函数,那么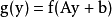 也是凹函数。
也是凹函数。
等等性质。
注某些教材的凹函数定义与此定义相反,即凸函数与凹函数相反。如北京大学版本和中山大学的数学教材。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国