概述
实际构件中的裂纹往往不是单一型的,由于载荷不对称,结构不对称,或者裂纹的方位不对称以及材料各向异性等情况,常使得裂纹尖端附近区域的应力场里,同时掺杂着型Ⅰ和Ⅱ型甚至Ⅲ型裂纹的应力,这种裂纹称为复合型(亦称混合型)裂纹。在还没有提出复合型断裂判据之前,人们只好将复合型裂纹筒化为I型裂纹来处理,显然这是不符合实际的,因此,如何建立复合型裂纹的断裂判据,是工程上的一个重要问题。
人们通过观察,发现复合型受力裂纹与单纯张开型受力裂纹的主要不同之点是,裂纹的扩展并不是沿着原裂纹面方向,而是沿着与原裂纹面成某一角度的方向扩展。于是,对于复合型裂纹,主要在于确定两个问题:
(1)裂纹开始沿什么方向扩展?即需要确定开裂角(同原裂纹面方向的夹角);
(2)裂纹在什么时候开始扩展?即需要确定临界点。
为了回答这两个问题,已经提出了许多种复合型裂纹脆性断裂理论。这些断裂理论与材料力学中所介绍的强度理论一样,是建立在科学假设基础之上的。所谓科学的假设,它既不是定论,也不是空想,而是科学发展中的必然产物,它的正确与否取决于是否与实际情况相符合。1
基本原理最大拉应力理论(亦称最大周向应力理论),有两个基本假设:
(1)裂纹沿周向应力取得最大值的方向开始扩展;
(2)裂纹的扩展是由于最大周向应力达到了临界值而产生的。
第一个假设可以求得开裂角,第二个假设可以确定临界点。根据迭加原理,Ⅰ-Ⅱ复合型裂纹尖端附近的极坐标应力场为:
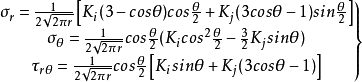
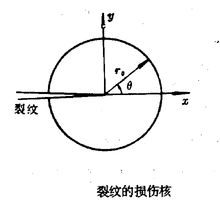
由于在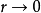 的裂纹尖端处,各应力分量趋于无限大,所.以,在应用最大周向应力理论时不能考虑裂纹的尖端点,只能应用距裂纹尖端一微小距离
的裂纹尖端处,各应力分量趋于无限大,所.以,在应用最大周向应力理论时不能考虑裂纹的尖端点,只能应用距裂纹尖端一微小距离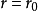 的圆周上各点处的周向应力
的圆周上各点处的周向应力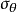 (图1),并由此得到开裂角
(图1),并由此得到开裂角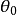 。
。
周向应力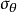 取得最大值的条件为
取得最大值的条件为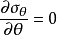 。
。
将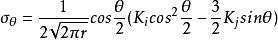 式子对
式子对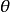 求导,若令
求导,若令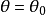 时,能满足
时,能满足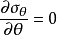 ,则有
,则有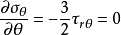 ,即
,即
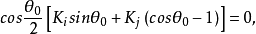 其中,由
其中,由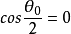 ,得出解
,得出解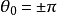 ,无实际意义。因此,开裂角
,无实际意义。因此,开裂角 决定于方程
决定于方程
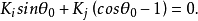
由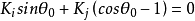 方程求出断裂角
方程求出断裂角 后,代入
后,代入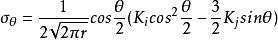 式子,即可求得
式子,即可求得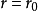 圆周上的最大周向应力为
圆周上的最大周向应力为
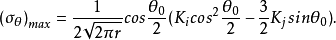
根据假设(2),可以建立起相应的开裂判据:
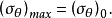
式中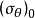 为最大周向应力的临界值,可以通过Ⅰ型裂纹的断裂韧性
为最大周向应力的临界值,可以通过Ⅰ型裂纹的断裂韧性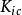 来确定。由于Ⅰ型裂纹在扩展时总是沿着原裂纹面的方向,因此,开裂角
来确定。由于Ⅰ型裂纹在扩展时总是沿着原裂纹面的方向,因此,开裂角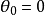 。将
。将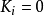 ,
,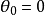 ,
,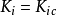 代入
代入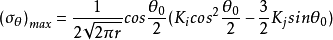 式子中,即可求得最大周向应力的临界值为
式子中,即可求得最大周向应力的临界值为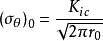 。
。
这就是按最大周向应力理论建立起来的Ⅰ-Ⅱ复合型裂纹的断裂依据。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国