方向导数导数
定义 设函数 在点
在点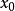 的某领域内有定义,若极限
的某领域内有定义,若极限
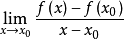
存在,则称函数 在点
在点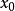 处可导,并称该极限为函数
处可导,并称该极限为函数 在点
在点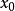 处的导数,记作
处的导数,记作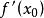 。
。
定义设三元函数 在点
在点 的某领域
的某领域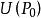 在
在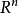 中有定义,
中有定义,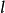 为从点
为从点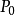 出发的射线,
出发的射线,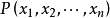 为
为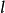 上且含于
上且含于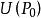 内的任一点,以ρ表示
内的任一点,以ρ表示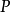 与
与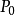 两点间的距离。若极限
两点间的距离。若极限
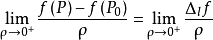 存在,则称此极限为函数
存在,则称此极限为函数 在点
在点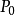 沿方向
沿方向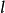 的方向导数1,记作
的方向导数1,记作
 或
或
方向导数与偏导数、全微分的关系定理1 多元函数 在点
在点 的某个领域
的某个领域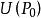 在
在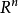 中有定义,且在点
中有定义,且在点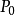 处可微,则在该点处 任意方向上的方向导数都存在,但反之不成立2。
处可微,则在该点处 任意方向上的方向导数都存在,但反之不成立2。
证:设向量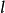 为从
为从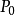 出发的射线,为
出发的射线,为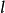 上且含于
上且含于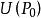 内的任一点,并以ρ表示
内的任一点,并以ρ表示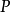 与
与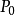 两点间的距离,由假设知多元函数
两点间的距离,由假设知多元函数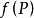 点
点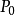 处可微,从而有:
处可微,从而有:
 也即有
也即有 存在,按照定义即证明了方向导数存在,且
存在,按照定义即证明了方向导数存在,且
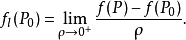
梯度定义若多元函数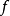 在点
在点 存在对所有自变量的偏导数,则称向量
存在对所有自变量的偏导数,则称向量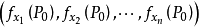 为函数
为函数 在点
在点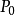 的梯度3,记作
的梯度3,记作
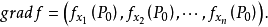
向量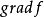 的长度(或模)为
的长度(或模)为
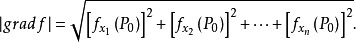
梯度与方向导数的关系
定理2 设多元函数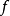 在点
在点 的某个领域
的某个领域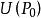 属于
属于 内有定义,且在点
内有定义,且在点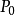 处可微。其中
处可微。其中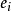 是
是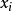 轴对应的单位向量。向量
轴对应的单位向量。向量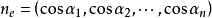 为向量
为向量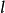 的方向余弦。则有
的方向余弦。则有
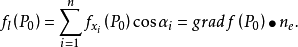
注:若多元函数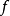 在点
在点 点可微,当
点可微,当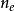 与
与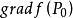 方向相同时,方向导数取得最大值
方向相同时,方向导数取得最大值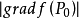 ,也即
,也即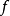 在
在 得梯度方向是其增长最快方向;当
得梯度方向是其增长最快方向;当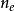 与
与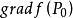 方向相反时,方向导数取得最小值
方向相反时,方向导数取得最小值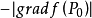 ,也即
,也即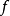 在
在 的梯度反方向是
的梯度反方向是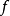 的值减少最快方向。
的值减少最快方向。
应用(1)设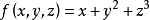 ,求
,求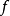 在点
在点 沿方向
沿方向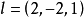 的方向导数。
的方向导数。
解:易见 在点
在点 可微。所以
可微。所以
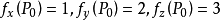 以及方向
以及方向 的方向余弦
的方向余弦
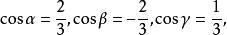
故
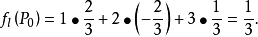
(2)设质量为m的质点位于原点,质量为1的质点位于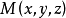 ,记
,记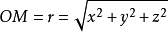 ,求
,求 的梯度。1
的梯度。1
解:

若以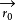 表示
表示 上的单位向量,则有
上的单位向量,则有
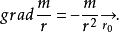




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国