概念
第一个张量对它的前两个指标是对称的,而第二个张量对前三个指标是对称的。若有这样的张量,它的两个反变指标或共变指标互换时,张量的分量值改变符号而大小不变,则该张量称为反对称或斜对称的。
因此,若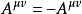 ,则:
,则:
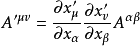
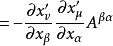
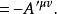
类似的,若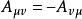 ,则
,则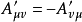 。这里
。这里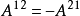 等等,而且
等等,而且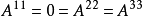 。因此运算分量数仅是
。因此运算分量数仅是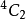 。1
。1
基本原理显然,反对称张量的分量满足关系式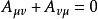 或
或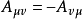 。这表明,当指标互换时,张量改变其符号。若
。这表明,当指标互换时,张量改变其符号。若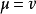 ,则给出
,则给出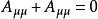 或
或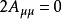 或
或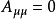 。
。
所以用下列系数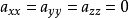 和
和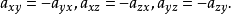 给出张量是反对称或斜对称的条件,若如图1所示,则φ是反对称的。
给出张量是反对称或斜对称的条件,若如图1所示,则φ是反对称的。
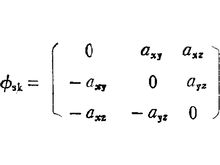
该矩阵只有三个分量,只有三个分量的性质为矢量所具有。这导出如下的结论: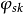 对矢量
对矢量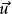 的运算完全相当于两个矢量的矢积,因为最后结果本身就是矢量
的运算完全相当于两个矢量的矢积,因为最后结果本身就是矢量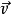 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国