[科普中国]-汤川理论

概述

带电粒子之间的力是通过电磁场的中间作用的，而电磁场又有时显出粒子性。电磁场的量子就是光子。电磁场理论的成功向人们提示了是否对核力也可以建立一种场的理论。1935年汤川秀树提出一种理论，说核子之间也通过一种场起作用，而这种场的量子是一种具有静质量的粒子，其静质量大约是电子质量的200倍。1936年在宇宙线中发现了一种粒子，后来称为子，其质量正是稍大于电子质量的200倍。当时以为汤川所说的粒子由此已经证实。后来逐渐搞清楚了子不符合汤川理论的要求。到了1947年另一种粒子被鲍威尔等发现，其质量是电子质量的273倍，称为介子，这才是汤川理论中的粒子。1

基本原理正如带电粒子之间的电磁场可以用势函数来描述，对核子之间的核力场也可以推得适当的势函数，并从而可以估计核力场的量子应有的静质量。下面我们对静介子场进行一些推算。

一个具有静质量和动量的自由粒子的哈密顿函数按照相对论是：

平方后成为：

用量子力学的算符，等代入，使运算于势函数，即得：

此式称克莱恩-戈登方程，适用于自旋为0的自由粒子。介子符合这个要求。

如果令上式中的，这公式就成为熟悉的电磁场公式。对静电场，式中对时间微商一项又等于零。如果在坐标的原点上有一固定的电荷，静电场的公式可列为：

式中，

其中，式子的解是：

如果离原点为的地方另有电荷，则两电荷的势能是：

相似的情况是静介子场，此时。仍设坐标的原点上有一核子，它带有相当于电荷的代表核力强度的量，那么势函数的方程是：

设，是球形对称的，上式可解出：

如果离原点为的地方有另一核子，两核子之间的势能是：

这个势能是负的，因为作用力是吸引力。

这个势函数随的增加急剧地趋于零，代表了短程力。当大于之术中的常数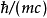时，力就很小，所以这个常数值就代表力程的数量级。另一方面，力程的数量级应该与原子核大小相仿。这样，

式中的是康普顿波长，把这些数值代入，就得：

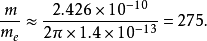这同介子质量的实验值很接近。2