概念
电荷共轭算符是与时-空连续无关的内禀对称性。狄拉克理论的粒子-空穴对称性和斯图克尔伯格(Stueckelberg)-费曼描述的粒子-反粒子对称性是提出电荷共轭算符的依据。当所有粒子被它们的反粒子所取代时,电荷共轭不变性要求物理定律保持不变,电荷共轭首先正式用于电子和正电子,而后来又推广应用于所有的粒子。1
基本原理电子场对应于荷电 和
和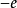 称为电子和正电子的两种粒子。习惯上把电子和正电子分别看成粒子和反粒子,我们下面证明,粒子和反粒子除了有相反的电荷外,它们还扮演了对称的角色。
称为电子和正电子的两种粒子。习惯上把电子和正电子分别看成粒子和反粒子,我们下面证明,粒子和反粒子除了有相反的电荷外,它们还扮演了对称的角色。
在存在相互作用的情况下,得出的电子场方程组是:
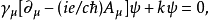
 如果我们在上式中用
如果我们在上式中用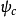 代替
代替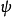 ,用
,用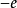 代替
代替 得:
得:
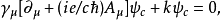
 用这一场方程组来代替
用这一场方程组来代替 和
和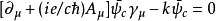 式,所得到的理论除了电子和正电子地位将交换外,和原来的理论是一样的。场算符
式,所得到的理论除了电子和正电子地位将交换外,和原来的理论是一样的。场算符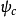 称为
称为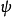 的电荷共轭。
的电荷共轭。
以上二组场方程可以互相变化。因为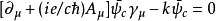 式的转置是:
式的转置是:
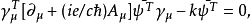 所以,在乘以有逆矩阵
所以,在乘以有逆矩阵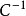 的常数矩阵
的常数矩阵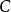 之后得:
之后得:
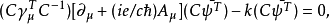 如果
如果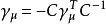 且
且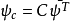 ,则它将和
,则它将和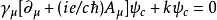 一致。根据矩阵表示有:
一致。根据矩阵表示有:
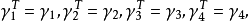 因此,将
因此,将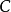 取为
取为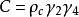 而
而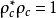 ,则
,则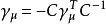 式可被满足。这里附加在常数
式可被满足。这里附加在常数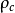 上的条件保证了
上的条件保证了 是幺正的。2
是幺正的。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国