信赖域算法的基本思想
在每次迭代中给出一个信赖域,这个信赖域一般是当前迭代点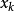 的一个小邻域。然后,在这个邻域内求解一个子问题,得到试探步长(trial step)
的一个小邻域。然后,在这个邻域内求解一个子问题,得到试探步长(trial step)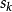 ,接着用某一评价函数来决定是否接受该试探步以及确定下一次迭代的信赖域。
,接着用某一评价函数来决定是否接受该试探步以及确定下一次迭代的信赖域。
如果试探步长被接受,则: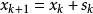 ,否则,
,否则,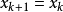 。
。
新的信赖域的大小取决于试探步的好坏,粗略地说,如果试探步较好,在下一步信赖域扩大或者保持不变,否则减小信赖域。
信赖域方法思想设当前点 的邻域定义为:
的邻域定义为: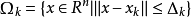 ,其中,
,其中,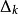 称为信赖域半径。
称为信赖域半径。
目标函数在极值点附近近似一个二次函数,因此对于无约束优化问题,利用二次逼近,构造如下信赖域子问题:
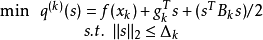
其中,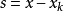 ,
,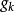 是目标函数
是目标函数 在当前迭代点
在当前迭代点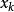 处的梯度,
处的梯度,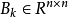 对称,是
对称,是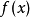 在
在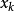 处Hesse阵
处Hesse阵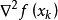 或者其近似。
或者其近似。
设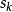 是信赖域子问题的解。目标函数
是信赖域子问题的解。目标函数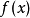 在第
在第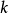 步的实际下降量(真实下降量):
步的实际下降量(真实下降量):
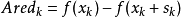
二次模型函数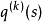 的下降量(预测下降量):
的下降量(预测下降量):
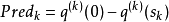
定义比值:
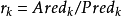
它衡量了二次模型与目标函数的逼近程度,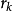 越接近于1,表明接近程度越好。因此,我们也用这个量来确定下次迭代的信赖域半径1。
越接近于1,表明接近程度越好。因此,我们也用这个量来确定下次迭代的信赖域半径1。
信赖域半径的选择(1)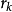 越接近与1,表明接近程度越好。这时可以增大
越接近与1,表明接近程度越好。这时可以增大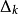 以扩大信赖域;
以扩大信赖域;
(2)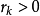 但是不接近于1,保持
但是不接近于1,保持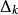 不变;
不变;
(3)如果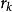 接近于0,减小
接近于0,减小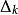 ,缩小信赖域。
,缩小信赖域。
信赖域算法的步骤Step1:给出初始点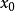 ,初始信赖域半径
,初始信赖域半径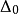 ,开始迭代2。
,开始迭代2。
Step2:到第k步时,计算梯度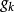 与Hesse阵
与Hesse阵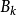 。
。
Step3:求解信赖域模型,得到试探步长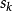 ,计算比值
,计算比值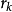 。
。
Step4:若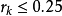 ,说明步子迈得太大了,应缩小信赖域半径,令
,说明步子迈得太大了,应缩小信赖域半径,令 。
。
Step5:若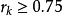 且
且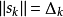 ,说明这一步已经迈到了信赖域半径的边缘,并且步子有点小,可以尝试扩大信赖域半径,令
,说明这一步已经迈到了信赖域半径的边缘,并且步子有点小,可以尝试扩大信赖域半径,令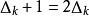 。
。
Step6:若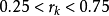 ,说明这一步迈出去之后,处于“可信赖”和“不可信赖”之间,可以维持当前的信赖域半径,令
,说明这一步迈出去之后,处于“可信赖”和“不可信赖”之间,可以维持当前的信赖域半径,令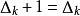 。
。
Step7:若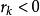 ,说明函数值是向着上升而非下降的趋势变化了(与最优化的目标相反),说明这一步迈得错得“离谱”了,这时不应该走到下一点,而应“原地踏步”,即
,说明函数值是向着上升而非下降的趋势变化了(与最优化的目标相反),说明这一步迈得错得“离谱”了,这时不应该走到下一点,而应“原地踏步”,即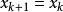 ,并且和上面
,并且和上面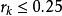 的情况一样缩小信赖域。反之,在
的情况一样缩小信赖域。反之,在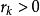 的情况下,都可以走到下一点,即
的情况下,都可以走到下一点,即 。
。
信赖域算法的收敛性信赖域算法具有整体收敛性2。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国