[科普中国]-德鲁克－普拉格准则

概述关于强度准则

强度准则的建立是为了反映岩石的破坏机理。岩石的破坏，通常可以分为脆性破坏和延性破坏。前者特点是岩石达到破坏时不产生明显的变形，后者的特点是破坏时会产生明显的塑性变形而不呈现明显的破坏面。岩石之所以能产生脆性或延性破坏，除了受到应力及应力状态影响外，也受到温度、应变率，地质构造等因素的影响，但目前大多数岩石破坏准则仅仅认为与应力或应变状态有关。在单向应力状态时，岩石破坏准则可以直接通过岩石力学实验获得。例如采用破坏时的最大应力作为破坏判据，但一般在地层中，岩石是处于三向应力状态的，而岩石的破坏往往与三个主应力大小及其相互间的比值有关。1

德鲁克－普拉格的岩石破坏准则M-C准则体现了岩土材料压剪破坏的实质，所以获得广泛的应用。但这类准则没有反映中间主应力的影响，不能解释岩土材料在静水压力下也能屈服或破坏的现象。

德鲁克和普拉格于1952年提出了考虑静水压力影响的广义Mises屈服与破坏准则，常常被称为德鲁克－普拉格准则,简称D-P准则，即：

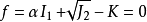式中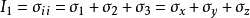， 为应力的第一不变量；

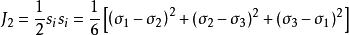为应力偏量第二不变量；α，K为与岩石内摩擦角和粘结力有关的实验常数。

D-P准则计入了中间主应力的影响，又考虑了静水压力的作用，克服了M-C准则的主要弱点，已在国内岩土力学与工程的数值计算分析中获得广泛的应用。2

德鲁克-普拉格岩石强度准则的修正德鲁克一普拉格准则岩石力学中最为重要的强度理论之一，在岩土工程研究中，尤其是在岩土工程数值分析中应用极为广泛，该强度理论同时反映了体积应力、剪应力和中间主应力力对岩石强度的影响，较比它强度理论更能反映实际。然向，工程实际应用表明该强度理论较为保守，以此作为依据进行工程设计计算，，其经济性值得考虑，有必要对该强度理论进行合理修正。

本构模型的建立利用Lemaitre J[9]应变等价性假说，可以建立岩石损伤本构关系

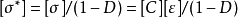式中：[C]为岩石材料弹性矩阵；[σ*]为有效应力矩阵；[σ]为名义应力矩阵；[ε]为应变矩阵；D为岩石损伤变量。

过去大多用岩石轴向主应变来表示岩石微元的强度[3,4]，作者认为它不能反映复杂应力状态对岩石微元 强度的影响。因此，基于Drucker-Prager破坏准则，提出岩石微元强度F*的表示方法

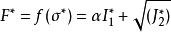
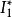
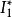式中：α为与岩石粘聚力c和内摩擦角φ有关的参数,I*1为应力张量的第一不变量，I*1=σ*1+σ*2+σ*3；J*2为应力偏量的第二不变量，J*2=[(σ*1-σ*2)^2+(σ*2-σ*3)^2+(σ*1-σ*3)^2]/6，σ * 1、σ*2、σ*3为有效应力。3

本构模型的修正不同的围压或者不同的复杂应力状态对岩石破裂过程损伤本构关系的影响是不同的，为了使上述所建 立的模型具有一般性，必须对此模型进行修正，其修正方法必须反映岩石应力与应变关系曲线的特点，因此有必要探讨前述岩石损伤统计本构模型参数的变化规律。

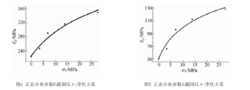
参数F0与S0反映了岩石变形的力学性质，如图2、图3所示。由图中可以看出：(1)岩石的应力应变曲线 的峰值随F0与S0的增大而增大，但是，F0与S0的变化并不改变峰值前线性变形曲线；(2)F0与S0对岩石应力应 变曲线的非线性变形部分，尤其是峰值后曲线影响是明显的，可以改变曲线的形态。上述两个特点反映了 F0与S0对岩石应力应变曲线的影响。

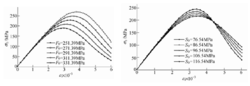
大量试验曲线表明，不同围压下岩石全应力应变曲线存在如下普遍特点：(1)岩石全应力应变曲线的 峰值随围压的变化而变化，峰值前应力较高的非线性部分与峰值后软化曲线部分同样随围压变化而变化； (2)峰值前低应力线性部分并不随围压的变化而变化。对岩石损伤软化统计本构模型进行修正也必须反映 上述特点。

对比前述得到的F0、S0对岩石损伤统计本构模型影响的特点与规律，可以看出，如果能建立起F0及S0 与围压σ3的关系，那么就能比较有效地对岩石损伤统计本构模型进行修正。考察根据前述方法得到的文献(周维垣，吴澎，杨若琼.节理岩体的损伤模型[A].岩石力学新进展[C].沈阳：东北工学院出版社,1989. )中不同围压下岩石应力应变试验曲线的统计损伤本构方程参数F0与S0，如果分别以F0与S0为纵坐标，围 压σ3为横坐标，即可得到F0-σ3与S0-σ3散点分布图，见图4和图5。