定义
随着系统生物学的快速发展,布尔动态模型作为分析基因间相互作用的有效工具,迅速成为系统生物学家们研究的热点问题。由于布尔控制网络可较好的模拟基因调控网络,因而布尔控制网络的研究在系统生物学领域和控制科学领域引起了广泛的关注。
近年来,程代展及其团队提出了矩阵半张量积运算,这为布尔控制网络的研究提供了新的理论工具。运用矩阵半张量积,布尔控制网络的逻辑动态方程转化为双线性方程,这大大推动了布尔控制网络的发展。
布尔控制网络代数表示
令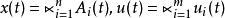 ,
,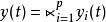 。
。
布尔控制网络的线性表示如下
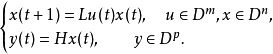
性质一、布尔网络的能控及能观性研究
1、布尔控制网络能控性
对于一个布尔控制网,给定初始状态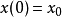 和目标状态
和目标状态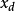 ,
,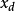 被称为是从
被称为是从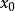 可以可控制的(经s步)使用确定的输入结构图
可以可控制的(经s步)使用确定的输入结构图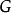 ,如果我们可以找到
,如果我们可以找到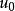 (和
(和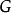 ),使得
),使得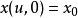 并且
并且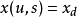 对于固定的
对于固定的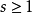 。
。
2、布尔控制网络能观性
布尔控制网络是可观测的,如果任何初始状态x0至少存在一个布尔值控制序列,使得可以通过输出序列确定初始状态。
文献1最先提出了布尔控制网络能控性和能观性的定义。随后,文献2用输入-状态关联矩阵的方法研究了布尔网络的能控性和能观性。基于2,各种类型布尔控制网络的能控性和能观性被讨论,包括:状态受限布尔控制网络345,概率布尔控制网络6,切换布尔控制网络7,髙阶布尔控制网络8,奇异布尔控制网络[9,时滞布尔控制网络10。
二、布尔网络的局限性
由于绝大多数布尔控制网络都不具有树形结构,而且对大多数基因调控网络而言,过多的忽略基因会严重影响估计值的精度,因而这些方法都具有局限性。所以,在研究布尔网络模型时,如何寻找有效的方法来降低算法的复杂度仍然是一个具有挑战性的问题。
应用布尔控制网络的应用。布尔控制网络代数表达式的提出为许多问题的研究提供了新的方法,例如:符号动力学,演化博弈,移位寄存器的奇异性,奇异布尔控制网络,染色问题,辨识问题,模糊线性规划问题,有限自动机,电路检测等。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国