[科普中国]-修正剑桥模型

产生及推导剑桥模型

剑桥模型是英国剑桥大学的Roscoe和Burland根据正常固结粘土和弱超固结粘土的三轴试验，采用状态边界面的概念，由塑性理论的流动法则和塑性势理论，采用简单曲线配合法，建立塑性与硬化定律的函数。它考虑了静水压力屈服特性、压硬性、剪缩性，但破坏面有尖角，该点的塑性应变方向不易确定。其假定的弹性墙内加载仍会产生塑性变形。

试验证明，对于正常固结粘土和弱固结的饱和重塑粘土，孔隙比e与外力p，q之间存在有唯一的关系，且不随应力路径而发生变化（这是通过p为常数的试验、固结排水试验和固结不排水试验，得出的试验破坏结果在p-q上的投影点连线斜率相等推导得出的），这个面叫作边界状态面。它可以看作由无数条不同应力比（p/q）的正常压缩曲线组成的。剑桥模型在e-p-q空间坐标的图形如图1。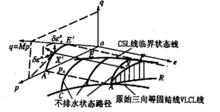

图1中ACEF就是状态边界面的一部分，AC线是在σ1=σ2=σ3（即q=0）时的e-p曲线，即为原始三向等压力固结线，简称为VICL线，而EF线是q为最大值各点的连线，称为临界状态线，简称为CSL线，它在p-q平面上的投影是通过原点的一条直线：q=Mp，对于正常压密粘土，考虑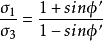到 ，可得到 ，EF线在e-p曲线上的投影为e=ea-λlnp，而AC和EF之间为一系列的不同应力比的曲线，将这些曲线绘制在e-lnp平面上，就构成了斜率均为λ的直线。同理，当正常固结压缩状态卸荷时，可得到不同应力比的回弹曲线，膨胀曲线在e-lnp平面上的投影时一系列的斜率为k的平行直线。从正常压缩状态卸荷，状态边界面为与q无关的铅直面，称为弹性墙，弹性墙与状态面有一交线，该交线在p-q平面上的投影曲线称为屈服轨迹，其方程为屈服函数。2

修正剑桥模型的推导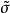 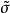修正剑桥模型也是建立在状态面理论基础上的，其所用强度理论为扩张Mises准则。但是，大量的研究结果表明，一般的岩土材料并不服从扩张Mises准则。通过应力变换的方法，将σ应力空间中的松冈-中井准则（如图2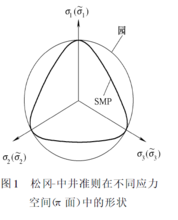）变换到应力空间中，使变换后的松冈-中井准则（SMP准则）在的主应力空间中具有和剑桥模型的广义Mises准则一样的形状，从而，可以使SMP准则和修正的剑桥模型有机地融为一体，这种通过应力变换方法得到的融合修正剑桥模型称为SMP修正剑桥模型。所用的应力空间变换关系为

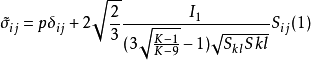
式中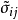： 为变换应力张量；I1为第一应力不变量；Sij为偏差应力张量；p为平均应力；δij为单位张量；K可以写成K=I1I2/I3，其中I1、I2和I3分别为3个应力不变量。

因此, 修正剑桥模型在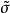 应力空间中的屈服函数可以表示为

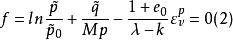
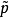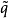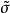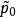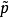式中： 和 为 应力空间中的平均有效应力和剪应力； 为 的初值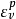； 为塑性体积应变，是该模型的一个状态量；M、e0、λ和κ是该模型的材料参数。

下面根据子负荷面的研究成果，在SMP修正剑桥模型中追加一个反映超固结土变形特性的状态量lnROC , 则屈服函数式（2）可以改写成

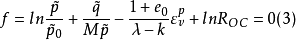
式中：ROC为土的超固结比，对于正常固结黏土ROC=1，屈服函数和式（2）完全一致。

根据塑性理论, 屈服函数式（3）的Prager一致性条件（Consistency Condition）可以表示为

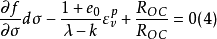状态量ROC的演化规则可以假定如下

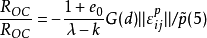
式中：G(d)= ad2

a为模型的材料参数；d 为超固结比的函数，可以表示为，d =(λ-κ)lnROC；塑性应变速率可以表示为，

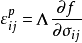
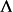为塑性乘子。

传统的单屈服面模型只可能反映卸载时的弹性变形和加载时的塑性硬化变形，不可能反映应变软化情况。3

三轴试验验证先将饱和的藤森黏土试样加压进行等向固结，然后，卸载使试样达到一定的超固结比，最后，在保持平均有效应力一定的条件下，加载使试样达到剪切破坏为止。为了检验本文的模型，分别设计了OCR等于1、2、4和8的藤森黏土三轴压缩和伸长剪切试验方案，其中，OCR=8的试验方案由于受加载条件的限制，采用较小的平均有效应力，为98kPa，其余3个试验方案的平均有效应力全部为196kPa。三轴压缩试验为施加轴向应力、减少室压使平均有效应力保持不变，三轴拉伸试验则为施加室压、减少轴向压应力使平均有效应力在整个试验过程中保持不变。3

总结扩展后的修正剑桥模型所用的材料参数和剑桥模型一样，可以利用简单的固结试验和小主应力保持恒定的排水剪试验确定。

图3中分别表示OCR等于1、2、4和8的藤森黏土在平均有效应力p一定条件下的三轴压缩试验结果（Observed）和SMP修正剑桥模型预测结果，为了便于和中井的子负荷面模型进行比较，图中同时给出了中井子负荷面模型的预测结果（Tij）。横坐标表示剪切应变，纵坐标的左、右两轴分别表示剪应力和平均应力之比及体积应变。从图3可以看出，扩展后的SMP修正剑桥模型可以用较少的模型参数，较好地反映超固结黏性土的体积剪胀特性和正常固结土的体积剪缩特性。同时，这个结果和三轴试验结果接近，剪应力比曲线也和三轴试验结果相近，说明扩展后的SMP修正剑桥模型可以用于超固结黏性土的应力、应变分析中。另外，从图中还可以看出，中井的子负荷面模型比SMP修正剑桥模型有更高的精度，其中的主要原因是因为两个模型所采用的剪胀关系有一定的差异。

图4中分别表示OCR等于1、2、4和8的藤森黏土在平均有效应力p一定条件下三轴伸长的试验结果和SMP修正剑桥模型预测结果。从图4可以看出，该SMP修正剑桥模型同样可以较好地反映超固结黏土在伸长应力路径下的体积剪胀特性和正常固结土的体积剪缩特性，并且和三轴试验的结果接近。

结论

为了使SMP修正剑桥模型能够反映超固结黏性土的强度和体积剪胀特性，利用子负荷面本构模型的最新研究成果在原屈服函数中加入了一个描述超固结黏土的变形和强度特性的参数（超固结比），同时，假定了超固结比随塑性应变而变化的演化规则，最后，通过和三轴试验结果及中井的子负荷面模型预测结果的比较，得到了如下结论：

（1）扩展SMP修正剑桥模型可以反映正常固结土的体积剪缩特性和超固结土的体积剪胀特性。该模型不仅对预测三轴压缩试验结果有效，而且对预测三轴伸长试验结果同样有效。

（2）扩展后的修正剑桥模型只增加一个和超固结比的演化有关的材料参数，模型其它参数的确定方法及具体数值和原剑桥模型一致。

（3）该扩展SMP修正剑桥模型形式简单，可以用于一般超固结土的应力应变数值分析。

（4）SMP修正剑桥模型虽然对模型所用破坏准则进行了修正，但是，剪胀关系还是沿用了原来模型中的形式。3