[科普中国]-量化系统

量化系统

在数字信号处理领域，量化指将信号的连续取值（或者大量可能的离散取值）近似为有限多个（或较少的）离散值的过程。量化系统（Quantitative System）是指将信号的连续取值（或者大量可能的离散取值）近似为有限多个（或较少的）离散值的系统，主要应用于从连续信号到数字信号的转换中。连续信号经过采样成为离散信号，离散信号经过量化即成为数字信号。注意离散信号通常情况下并不需要经过量化的过程，但可能在值域上并不离散，还是需要经过量化的过程 。信号的采样和量化通常都是由ADC实现的。1

所研究的量化系统的模型示于图1。模拟源的输出是高斯随机过程的样本函数a(f)。我们先假定消息过程具有带限谱：

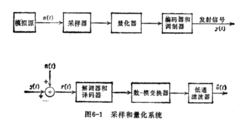
因为谱是带限的，我们可每1/2WM/秒采样一次而不丢失任何信息。由于过程是高斯的，且为平坦谱，采样值是统计独立的高斯随机变量O。每个采样值为零均值，单位方差。

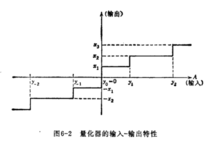
所谓量化，就是把经过抽样得到的瞬时值将其幅度离散，即用一组规定的电平，把瞬时抽样值用最接近的电平值来表示。经过抽样的图像，只是在空间上被离散成为像素(样本)的阵列。而每个样本灰度值还是一个由无穷多个取值的连续变化量，必须将其转化为有限个离散值，赋予不同码字才能真正成为数字图像。这种转化称为量化。

量化分类无论是将样本连续灰度值等间隔分层的均匀量化，还是不等间隔分层的非均匀量化，在两个量化级(即称之为两个判决电平)之间的所有灰度值用一个量化值(称为量化器输出的量化电平)来表示。

均匀量化和非均匀量化

按照量化级的划分方式分，有均匀量化和非均匀量化。

均匀量化：ADC输入动态范围被均匀地划分为2^n份。

非均匀量化：ADC输入动态范围的划分不均匀，一般用类似指数的曲线进行量化。

非均匀量化是针对均匀量化提出的，因为一般的语音信号中，绝大部分是小幅度的信号，且人耳听觉遵循指数规律。为了保证关心的信号能够被更精确的还原，我们应该将更多的bit用于表示小信号。

常见的非均匀量化有A律和μ率等，它们的区别在于量化曲线不同。

标量量化和矢量量化

按照量化的维数分，量化分为标量量化和矢量量化。标量量化是一维的量化，一个幅度对应一个量化结果。而矢量量化是二维甚至多维的量化，两个或两个以上的幅度决定一个量化结果。

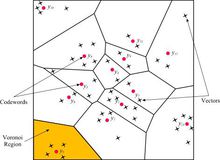
以二维情况为例，两个幅度决定了平面上的一点。而这个平面事先按照概率已经划分为N个小区域，每个区域对应着一个输出结果（码书，codebook）。由输入确定的那一点落在了哪个区域内，矢量量化器就会输出那个区域对应的码字（codeword）。矢量量化的好处是引入了多个决定输出的因素，并且使用了概率的方法，一般会比标量量化效率更高。

量化相关模数转换器(ADC)与数字电路中的量化

模拟信号数字化过程的一个步骤。即将采样的点转化为分散的值

数字电路中，采样和量化过程由A/D转换器完成。A/D转换器(ADC)一般为标量均匀量化。量化的过程就是把采集到的数值（称为采样值或样值，英语sample）送到量化器编码成数字形式（一般为二进制）。每个样值代表一次采样所获得的信号的瞬时幅度。

量化级量化器设计时将标称幅度划分为若干份，称为量化级，一般为2的整数次幂。把落入同一级的样本值归为一类，并给定一个量化值。量化级数越多，量化误差就越小，质量就越好。例如8位的ADC可以将标称输入电压范围内的模拟电压信号转换为8位的数字信号。

量化误差量化过程存在量化误差，在还原信号的D/A转换后，这种误差作为噪声再生，称为量化噪声。增加量化位数能够把噪声降低到无法察觉的程度，但随着信号幅度的降低，量化噪声与信号之间的相关性变得更加明显。

量化系统的复杂度控制在许多实际运用场合，码本的容量和码字矢量的长度都很大，那么，在编码的过程中，不可避免地带来很大的计算复杂度。输入矢量需要和码本中的所有码字计算相互间的距离，同时还要进行距离大小的比较，计算量很大。在要求实时计算的场合，这种由于计算所带乎的延时是不能接受的。同时，大容量的码本和很长的码字也会增加系统的存储容量。因此，工程技术人员想了一系列的方法来降低系统的计算复杂度，这些方法大致可以分为两类：无记忆的矢量量化系统和有记忆的矢量量化系统。2

无记忆的矢量量化系统无记忆的矢量量化系统降低系统复杂度的方法主要有两种：一是改变搜索算法，降低苎苎竺复杂度；二是改进系统的结构，从而改变码字的结构，使码字变短，码本容量变小苎降低计算复杂度和减小存储空间。前一种策略的典型代表是基于二叉树结构的搜索算法，后一种策略的代表是矢量量化系统的级联。

基于二叉树搜索的矢量量化系统二叉树搜索算法是数据结构中常见的快速搜索算法，工程技术人员将它应用到编码的过程中以改进系统的运算速度。也有的系统采用N叉树的结构，但思想上大同小异。图以8码字的码本为例，给出了系统搜索算法示意图。

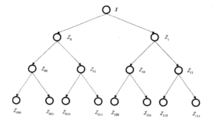
图中，8个叶结点是初始码本中的8个码字，其余的被称作附加码字，供搜索比较使用。首先，在原有的8个码字中寻找最接近的四对邻居，每对邻居算出一个中心点，得到序列Z00~Z11，然后，在新生成的四个码字中同样寻找邻居对并计算它们各自的中心，得到Z0~Z1。比较时，首先计算输入矢量X和Z0~Z1的距离，沿距离小的一支向下搜索，直到叶结点结束。采用基于二叉树的搜索算法，共需进行6次失真度计算和3次比较计算，而全搜索算法需要8次失真度计算和7次比较运算。但是，基于二叉树的搜索算法不能保证从码本中找到具有最小失真度的输出矢量，一定程度上降低了系统的性能，同时，附加码字的引入也增加了系统的存储量。

多级矢量量化系统多级矢量量化系统的工作原理是：

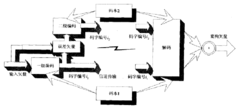
首先用一个小容量的码本来较为粗略地逼近输入矢量，码字编号为小同时在计算过程中保留逼近所带来的失真误差。然后，系统用另一个小容量的码本对失真误差进行再次量化，码字编号为i1。依次进行下去，根据实际运用的需要，可以人为地设置系统的级联次数秃。码字编号序列被用于传输和存储。整个系统的性能相当于一个码本容量为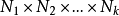的单级矢量量化系统。由于级联系统中每级码本容量都较小，因此搜索复杂度降低。图5给出一个两级矢量量化系统的系统结构图。多级矢量量化也有着其自身的弱点；随着级联数目的增加，系统性能效果增加不再明显，很快地趋于饱和。