概念
处于物理空间dV体积元内动量值小于p的电子,对应的相空间体积等于 .。这个体积中的"相格",亦即可能态的数目,等于
.。这个体积中的"相格",亦即可能态的数目,等于 ,这些态中的电子数在任何时刻都不能超过下列数值:
,这些态中的电子数在任何时刻都不能超过下列数值:

(每一“相格”中只能装进自旋相反的两个电子).在基态原子中,每一个dV体积元内的电子必须填满(相空间内的)动量值从零直到某一极大值 为止的相格.此时,电子动能在每一点都取尽可能小的数值.如果把dV体积元内的电子数写成ndV(n为电子数密度),那么,各点处电子动量的极大值
为止的相格.此时,电子动能在每一点都取尽可能小的数值.如果把dV体积元内的电子数写成ndV(n为电子数密度),那么,各点处电子动量的极大值 与n的关系为
与n的关系为

在电子数密度为n的地方,一个电子的最大动能值因而等于
 (1)
(1)
其次,设 为静电势,假定它在无穷远处等于零.电子的总能量为
为静电势,假定它在无穷远处等于零.电子的总能量为 .显然,每个电子的总能量一定等于负值,否则它会运动到无穷远处去.我们用
.显然,每个电子的总能量一定等于负值,否则它会运动到无穷远处去.我们用 代表每点处电子总能量的极大值,
代表每点处电子总能量的极大值, 是一个正的常数;如果
是一个正的常数;如果 不是常数的话,电子就会从
不是常数的话,电子就会从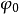 较小之处运动到
较小之处运动到 较大之处.因此我们可写出
较大之处.因此我们可写出
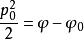 (2)
(2)
把(1)和(2)式等同起来,即得
 (3)
(3)
这就是原子内各点的电子数密度与势能的关系式.
 时,密度n等于零;在
时,密度n等于零;在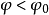 的整个区域内,显然也应令n,等于零,否则(2)式将会给出负的动能极大值.因此,方程式
的整个区域内,显然也应令n,等于零,否则(2)式将会给出负的动能极大值.因此,方程式 确定了原子的边界.但是,在总电荷为零的球对称电荷分布的外面并不存在电场.因此在中性原子的边界上应该有
确定了原子的边界.但是,在总电荷为零的球对称电荷分布的外面并不存在电场.因此在中性原子的边界上应该有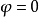 .由此得出结论,对中性原子讲来,常数
.由此得出结论,对中性原子讲来,常数 一定要等于零.反之,离子的常数
一定要等于零.反之,离子的常数 并不等于零.
并不等于零.
下面我们考虑中性原子,因而令 .根据静电学中的泊松方程,我们有
.根据静电学中的泊松方程,我们有 ;把(3)式代入这个式子,即得托马斯一费米方法的基本方程:
;把(3)式代入这个式子,即得托马斯一费米方法的基本方程:
 (4)
(4)
基态原子的电场分布是由上式的球对称解确定的,这个解应该满足以下的边界条件: 时,
时, 必须变成核库仑场,即
必须变成核库仑场,即 ;而当
;而当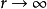 时,必须有
时,必须有 .引进下式定义的新变量x代替变量r:
.引进下式定义的新变量x代替变量r:
 (5)
(5)
并引进下列新的未知函数 代替
代替 :
:
 (6)
(6)
我们得到方程式
 (7)
(7)
其边界条件为x=0时 以及
以及 时疋
时疋 .这个方程不再含有任何参量,因而定义出一个普适的
.这个方程不再含有任何参量,因而定义出一个普适的 函数.下表给出了(7)式数值积分后所得的
函数.下表给出了(7)式数值积分后所得的 函数值.
函数值.

 函数是单调递减的,并且只在无穷远处等于零.换句话说,托马斯一费米模型中的原子并不存在边界,形式上延伸到无穷远处.
函数是单调递减的,并且只在无穷远处等于零.换句话说,托马斯一费米模型中的原子并不存在边界,形式上延伸到无穷远处.
导数 在r=0处的值等于
在r=0处的值等于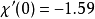 .因此当
.因此当 时
时 函数具有
函数具有 的形式,相应的势
的形式,相应的势 为:
为:
 (8)
(8)
第一项是核场的势,第二项是电子在原点的势(通常的单位制中为 ),把(6)代入(3)中,可得电子数密度的下列表式:
),把(6)代入(3)中,可得电子数密度的下列表式:
 (9)
(9)
1
解析我们看到,按托马斯一费米模型,不同原子中的电荷密度分布是相似的,并以 为特征长度(在通常的单位制中为
为特征长度(在通常的单位制中为 即玻尔半径除以
即玻尔半径除以 ).如果以原子单位量度距离,那么,电子数密度达到最大值的那个距离对所有的z都是一样的。因此可以这样说,原子序为Z的原子中大多数的电子与原子核的距离约为
).如果以原子单位量度距离,那么,电子数密度达到最大值的那个距离对所有的z都是一样的。因此可以这样说,原子序为Z的原子中大多数的电子与原子核的距离约为 的数量级。数值计算表明,原子中电子总电荷的一半处于半径为
的数量级。数值计算表明,原子中电子总电荷的一半处于半径为 的球内。
的球内。
同样的考虑表明,原子中电子的平均速度(与能量的平方根同一数量级)约为 的数量级.
的数量级.
托马斯一费米方程在远离原子核以及靠近原子核处都不能适用.它在近距离处的适用范围,由不等式 (远大于第一玻尔“半径”的距离)所限制;距离更小时,准经典近似在核库仑场内不再成立.令式
(远大于第一玻尔“半径”的距离)所限制;距离更小时,准经典近似在核库仑场内不再成立.令式 中的
中的 ,我们求得距离r的下限为1/Z.在复杂原子中,当r很大时准经典近似也不能成立.容易证明,当
,我们求得距离r的下限为1/Z.在复杂原子中,当r很大时准经典近似也不能成立.容易证明,当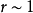 时,电子的德布罗意波长与距离本身成为同一数量级,准经典条件无疑遭到破坏.这一点,由估计(2),(4)式各项之值可以确信;实际上,由于(4)式不含Z,这个结论无需计算就能明显看出来.
时,电子的德布罗意波长与距离本身成为同一数量级,准经典条件无疑遭到破坏.这一点,由估计(2),(4)式各项之值可以确信;实际上,由于(4)式不含Z,这个结论无需计算就能明显看出来.
由此可见,托马斯一费米方程的适用范围,局限在大于1/Z和小于1的距离内.事实上在复杂原子中,绝大多数的电子实际上都是处于这个适用范围内.
后一种情况表明,托马斯一费米模型中原子的“外边界”位于 处,也就是原子的线度并不依赖于Z.与此相应,外电子的能量亦即原子的电离势也与Z无关.
处,也就是原子的线度并不依赖于Z.与此相应,外电子的能量亦即原子的电离势也与Z无关.
借助于托马斯一费米方法,可以算出总的电离能E,即移掉中性原子内全部电子所必需的能量.为此目的,我们有必要算出具有托马斯一费米分布的原子内电荷的静电能;我们所求的总能量等于这个静电能的一半,因为在按库仑定律作用的多粒子系统中,它的平均动能等于平均势能的-1/2(根据位力定理).E和Z的依赖关系可以根据以下的简单考虑事先确定:在电荷为z的核场内运动的Z个电子,在与核的平均距离为 处的静电能,与
处的静电能,与 成正比.数值计算的结果为
成正比.数值计算的结果为 .这个对Z的依赖关系与实验数据很符合;可是系数的经验值接近于16.
.这个对Z的依赖关系与实验数据很符合;可是系数的经验值接近于16.
我们已经提到过,常数 取不等于零的正值时对应于电离原子。如果我们通过
取不等于零的正值时对应于电离原子。如果我们通过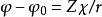 来定义
来定义 函数,所得的
函数,所得的 方程就和原先的(7)式相同。但是,我们现在感兴趣的不是在无穷远处等于零的中性原子那样的解,而是在有限值
方程就和原先的(7)式相同。但是,我们现在感兴趣的不是在无穷远处等于零的中性原子那样的解,而是在有限值 处等于零的解;这样的解,对任意一个
处等于零的解;这样的解,对任意一个 值讲来,都是存在的.在
值讲来,都是存在的.在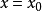 点处,电荷密度和
点处,电荷密度和 一起等于零,但是势能仍保持有限值.
一起等于零,但是势能仍保持有限值. 值可按以下方式与电离度相联系。按照高斯定理,半径为r的球内的总电荷等于
值可按以下方式与电离度相联系。按照高斯定理,半径为r的球内的总电荷等于 ,把
,把 代入上式,即得离子的总电荷z;由于
代入上式,即得离子的总电荷z;由于 ,故
,故
 (10)
(10)
图中的粗长曲线代表中性原子的 曲线;这条曲线的下面是两条电离度不同的离子的曲线。图中的z/Z值等于
曲线;这条曲线的下面是两条电离度不同的离子的曲线。图中的z/Z值等于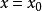 处曲线的切线在纵轴上的截距。
处曲线的切线在纵轴上的截距。

(7)式尚有任何处都不等于零的解;这些解在无穷远处是发散的。它可看作对应于负的常数 值。图中也画出了两条这样的
值。图中也画出了两条这样的 曲线;它们位于中性原子的曲线之上。在曲线的
曲线;它们位于中性原子的曲线之上。在曲线的 点处我们有
点处我们有
 (11)
(11)
在 的球内总电荷等于零(在图上,这一点显然就是切线通过原点的那个点)。如果在
的球内总电荷等于零(在图上,这一点显然就是切线通过原点的那个点)。如果在 点处把曲线截断,我们就定义了一个界面电荷密度不等于零的中性原子的
点处把曲线截断,我们就定义了一个界面电荷密度不等于零的中性原子的 .在物理上,这相当于束缚在某一给定有限体积内的“压缩”原子。
.在物理上,这相当于束缚在某一给定有限体积内的“压缩”原子。
托马斯一费米方程没有计及电子间的交换作用。这种作用的效应要比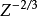 小一个数量级。因此,在托马斯一费米方法中计及交换作用时,还需同时计及同一数量级的其它各种效应。1
小一个数量级。因此,在托马斯一费米方法中计及交换作用时,还需同时计及同一数量级的其它各种效应。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国