[科普中国]-单位矢量

单位矢量的引入

如果质点沿着平面曲线C 运动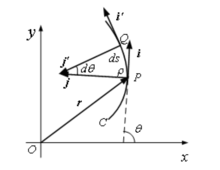，可以把加速度矢量a 分解为沿着轨道切线方向以及法线方向的两个分量。设曲线C 上某一点为弧长坐标s 的原点O，沿轨道切线一方向运动时，轨道弧长s 增加，沿轨道切线另一方向运动时，轨道弧长s 减小。i 为沿轨道切线方向并指向轨道弧长s 增加的方向上的单位矢量， j 为沿轨道法向并指向曲线凹侧的单位矢量，θ 为轨道前进的切线方向和x 轴之间的夹角，如图一所示。i 、j 和dθ之间满足下列关系式

质点速度为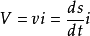 ，式中ds 是当 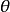改变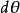 时，质点沿曲线C所移动的路程。在极限情况下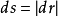， ,故 ,且弧长增加（即质点沿单位矢量i方向运动）时，ds > 0；

弧长减小时，ds

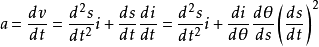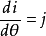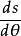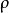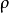因为 , ,，而此处则 等于曲线C 的曲率半径 ，又因 恒大于0，

故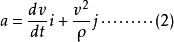

质点沿曲线C 运动的切向和法向加速度分量分别为：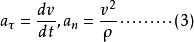

此式又称为内禀方程。

自然坐标系单位矢量的新认识在采用自然坐标系描述质点的平面曲线运动时，把加速度矢量a 分解为沿着轨道的切线以及法线方向两个分量。其中，法线加速度的方向一定指向曲线在该点的凹侧法线方向，这是由于质点法线方向受力的作用只改变质点速度的方向，而不改变质点速度的大小。在曲线的拐点处，法线加速度的大小为零。因此，法线方向的单位矢量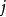 可以规定为沿轨道法向并指向曲线凹侧。对于沿轨道切线方向的单位矢量i ，我们将证明其方向可以任意规定。单位矢量i 正向的选取不会影响加速度矢量在自然坐标系中的表达形式，即沿轨道切线方向不论怎么选取单位矢量的正向，加速度矢量在自然坐标系中的表达形式都如公式（2）所示。我们考虑质点沿着正弦曲线运动的情况，

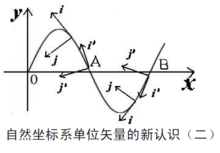如图二和图三所示。正弦曲线中既有凸的部分，也有凹的部分，同时还存在拐点。弧长坐标s 、单位矢量i 和j 的定义同上，θ 仍为轨道单位矢量i 的正向和x 轴之间的夹角。图二 和图三分别是沿轨道切线单位矢量i 正向选取的两种情况。

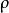综上所述，单位矢量i 正向的选取不会影响加速度矢量a 在自然坐标系中的表达形式。事实上， dθ 、ds 的正负以及i 、j 和dθ 之间的关系式取决于曲线的凹凸性和单位矢量i 正向的选取。在自然坐标系中，对于常用到的一些关系式，比如曲线在某点的曲率半径会根据dθ 、ds 的正负与ds / dθ 有相应的符号差别。此外，需要说明的是在靠近拐点时，ρ 趋于无穷大，法向加速度大小为零；又考虑到质点法线方向受力的作用只改变质点速度的方向，而不改变质点速度的大小，故在拐点两侧，法向单位矢量j 正向的突变对于求解质点曲线运动问题实质上没有影响。1

单位矢量正向的选取自然坐标系理论力学中对沿曲线运动的质点, 常把其加速度矢量a 分解为沿轨道的切线方向和法线方向的两个分量: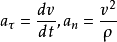.如果把轨道的切线和法线也作为坐标系来看,则叫自然坐标系。

选取方法切向坐标轴正向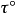的选取：沿轨道曲线的切线，并指向弧坐标的正方向。

法向坐标轴正向的选取:沿轨道曲线的主法线方向，即指向曲线的凹侧。2

注意：

( 1) 对于任意给定的光滑平面轨道曲线( 设曲线无拐点, 否则可分段考虑), 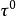在各点是唯一确定的, 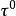沿曲线是逐点连续变化的。

(2) 自然系正法向单位矢禅的方向与曲线的正法向( 指向曲率中心), 沿曲线各点处处相同。

( 3) 不仅保持两式恒成立, 而且又有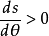恒成立,

于是就有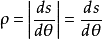恒成立。3