简介
电场中某点的位移电流密度等于该点的电位移矢量对时间的变化率。表达式如下:
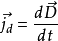
电位移矢量电位移矢量是在讨论静电场中存在电介质的情况下,电荷分布和电场强度的关系时引入的辅助矢量。即是一个用以描述电场的辅助物理量,用符号D表示。它的定义式为:
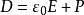
式中E是电场强度,P是极化强度,ε0是真空介电常数。D的单位是C/m²。对线性各向同性的电介质有D=εE,ε是电介质的绝对介电常数。电位移矢量又叫电感应强度矢量。
位移电流和位移电流密度的定义式根据麦克斯韦所提出的位移电流的概念,位移电流强度 和位移电流密度
和位移电流密度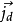 分别定义为 :
分别定义为 :
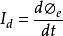
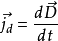
其中,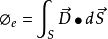 。
。
上述定义式说明,通过电场中的某截面的位移电流强度等于通过该截面的电位移通量的时间变化率;电场中某点的位移电流密度等于该点处电位移矢量的时间变化率。1
位移电流密度公式的一种导出方法位移电流密度公式 的导出在大多数电磁学教材里以及有关文献中都是用平行板电容器的充放电过程这个特例得出全电流公式,并指出全电流的连续性,以此得出位移电流密度公式。然而在教学中学生往往不易理解其物理含义,对位移电流的实质也认识不清,使学生认为只有传导电流为零的地方才由位移电流“接下去”。因此从电荷运动和场的变化的整体观念,运用高斯定律和电荷守恒定律来导出位移电流的密度公式,其推导过程本身对学生理解全电流的概念亦有帮助。
的导出在大多数电磁学教材里以及有关文献中都是用平行板电容器的充放电过程这个特例得出全电流公式,并指出全电流的连续性,以此得出位移电流密度公式。然而在教学中学生往往不易理解其物理含义,对位移电流的实质也认识不清,使学生认为只有传导电流为零的地方才由位移电流“接下去”。因此从电荷运动和场的变化的整体观念,运用高斯定律和电荷守恒定律来导出位移电流的密度公式,其推导过程本身对学生理解全电流的概念亦有帮助。
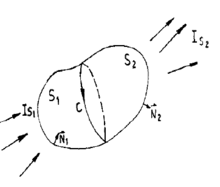
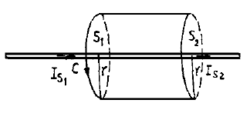
设S为空间任一闭合曲面,其法线向外,如图所示,C为S上一有向闭合曲线,分S为S1、S2两个曲面,按右手法则,S1的法线将指向内部,而S2的法线保持不变。设在此空间内有稳恒电流流动,在某时刻穿过S1面的电流为IS1,穿过S2面的电流为IS2,根据电荷守恒定律,不可能有电荷在S内积累或放出,所以,IS1= IS2。2
而根据安培环路定律,有: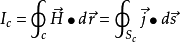 。
。
这里Sc是以C为边界的任何曲面,取SC为S1即得电流IS1,取Sc为S2即得IS2,所以在恒流情况下IS1= IS2是必然的。然而并不是在所有情形下在任何时刻穿过S1的传导电流IS1都与穿过S2的传导电流IS2相等。现考虑这样一种情况:
一根无限长的荷电直导线,以匀速V0沿其轴向运动,如果导线中电荷的分布是均匀的,其线密度为λ,那么对于静止的观察者来说,此即一无限长的通电长直导线,其电流强度为λV0,如图,我们选择以导线为轴线的圆柱面,S1、S2分别为圆柱面的两个底面,C为S1的边界线,即是一个绕圆柱的圆,由于是稳恒电流,所以IS1= IS2。然而若此无限长直导线荷电并非均匀,其荷电线密度随空间点x而变化,为λ(x),显然对于某一时刻传导电流IS1和IS2就不再相等,因为:
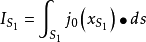
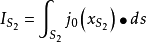
因为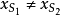 ,故
,故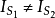 。
。
这样,穿过闭合曲线C的传导电流就不再是一个恒定的量,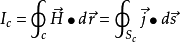 对于这种情形就不再适用了。对于我们所选的S1和S2来说,如某时刻穿过S1的传导电流为IS1,那么此时刻穿过S2的传导电流IS2相对IS1来说就会有所“增加”或“减少”,即是说在时间间隔dt内在S内有电荷积累或放出,显然此导线在空间建立的电场为一随时间而变化的场,对此运用高斯定律,则其电场的通量和所选曲面内导线中心的电荷积累和放出相关,因此,我们令:
对于这种情形就不再适用了。对于我们所选的S1和S2来说,如某时刻穿过S1的传导电流为IS1,那么此时刻穿过S2的传导电流IS2相对IS1来说就会有所“增加”或“减少”,即是说在时间间隔dt内在S内有电荷积累或放出,显然此导线在空间建立的电场为一随时间而变化的场,对此运用高斯定律,则其电场的通量和所选曲面内导线中心的电荷积累和放出相关,因此,我们令:
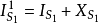
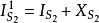
这里XS1、XS2是考虑到电荷的积累或放出而引起的所谓“动态修正”,由此,我们认为在这种非恒流情形下整个空间的“电流”仍然是恒定的话,就有: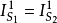 。
。
即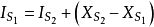 。
。
考虑对于S面的电荷运动情况,则: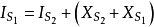
由电荷守恒定律,有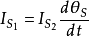 。
。
这里,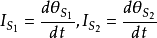 ,是某时刻流过S1和S2的传导电流,根据高斯定律,有
,是某时刻流过S1和S2的传导电流,根据高斯定律,有
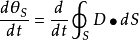
由于S1、S2的取法具有任意性,于是得到动态修正的表达式
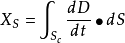
因此,我们考虑到空间电场的变化,则空间中的电流强度就应写成:
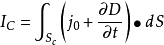
这样,电流密度公式就是:
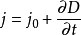




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国