[科普中国]-真空介电常量

简介

真空介电常量，又称为真空电容率，或称电常数，是一个常见的电磁学物理常数，符号为ε0。在国际单位制里，真空介电常量的数值为：

ε0=8. 854187817×10F/ m（近似值）。

历史背景如同前面所述，真空电容率是一个度量系统常数。它的出现于电磁量的定义方程，主要是因为一个称为理想化的程序。只使用纯理论的推导，麦克斯韦方程组奇异地预测出，电磁波以光速传播于自由空间。继续推论这个预测，就可以给出的数值。若想了解为什么会有这数值，需要阅读一下电磁度量系统的发展史。

在以下的讲述中，注意经典物理并不特别区分“真空”和“自由空间”这两个术语。当今文献里，“真空”可能指为很多种不同的实验状况和理论实体。在阅读文献时，只有上下文可以决定术语的含意。

基本概念真空介电常量是物理量在度量时引进的常数( 主要是库仑定律中对电荷量的度量) ，根据麦克斯韦方程组，可推知真空介电常数与其它物理常数的关系。

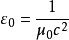
其中，c是光波传播于真空的光速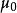， 是真空磁导率。上式可作为真空介电常数的定义式。

真空介电常数的本质物理上，真空介电常数是一个重要常数，用 ε0表示。

我们假设一正一负两电荷(电量为e)在相距距离为r的地方“静止”。其势能为：

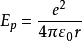
应指出，两电荷“静止”不代表其绝对静止，它们也在真空背景温度下悄悄运动。这个运动可看成简谐运动(也可用圆周运动来描述)，周期为t。因此，某个电荷要产生电流I，且I=e/t。

由于电荷运动其电场也跟着变化(指空间静止某点的电场强度变化)，又位移电流的本质是变化电场，所以这种变化的电场就会在两电荷之间传递，形成电流。此处的位移电流周期也为t，大小也为I=e/t。因为位移电流的表述式可写为：

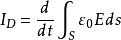
这里，E为电场强度，S为截面积，∫S为面积分。

式子右边的积分可等电量Q，因此此式仍满足I=dQ/dt的关系。而这里I=e/t是从I=dQ/dt定义式推出，因此，I=e/t，可表示这里的位移电流在空间分布的大小。

我们再根据相对性原理得出，任何物理规律都有相同的数学表达式，因此，某电流所受的电压(或电势)e/ε04πr 也应满足欧姆定律U=IR，U为电压，R为电阻。

又：R=ρl/s

其中，ρ为电阻率，l为电流长度，s为截面积。对两点电荷来说，l=r，s=2πr，因为位移电流的长度即为两电荷间距离。应注意的是，截面似乎应是球面积4πr，但其实不是。我们可作这样分析：假设左边电荷带正电，右边电荷带负电，又假设右边负电荷不存在时，左边正电荷的电场线是以球面积发散，我们把这个球面分为左、右两个半球面。当右边有了负电荷时，正电荷的电场线应该几乎全部向右边半球指向(因为正电荷指向左边的电场线，这时也会受负电荷影响，也会迂回向右指向)，又由于位移电流是变化电场，那么变化电场这种电流就几乎全集中在右边半球，而左边半球几乎无电流，那么左边半球面对电阻就应无贡献。因此，正电荷的电阻就应取右边半球，其截面为半个球面，即2πr(当然，也可用其它方法分析，结论一样)。

我们又知道，根据量子力学观点，导体的电阻是由其内部的杂质而引起，而对于真空来说，其中没杂质，因此，真空的电阻只有几何因素，没有物质结构因素(电阻率)，或者说真空没有电阻率这个概念，真空的电阻率可看作1，没有转化系数。对于两点电荷来说，其位移电流的电阻为：

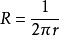
用这个电阻乘以单个电荷的电流I，有。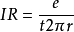

它等于受到的电压，有。

把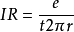代进去得：。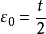

把t=1.762×10-11 代进去得：

这和实验值 ε0=8.85×10相比较，基本相符。说明了推导的可行性。

真空介电常数本质上应是时间的量纲。1

与真空背景周期的关系值得一提的是，t =8.81 ×10秒在数值上刚好近似等于真空介电常数ε0，这两个量之间有什么关系呢? 为了说明这个问题，这里假定真空中有二个带有相同电量( 电量为e) 的点电荷相互作用，相互作用势能为

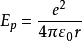
如果单个电荷以周期 t 做圆周运动，则电流强度为 I = e/t. 根据实验结果，电阻的表达式可写为：

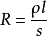
其中 ρ 为电阻率，l 为介质的长度，s 为介质的横截面积，电流的方向垂直于横截面。对两个点电荷来说，虽然它们“静止”，但它们受“真空背景温度”的影响，也在做轻微的热运动，这个运动可看成是简谐运动( 也可用圆周运动来进行描述) ，运动方向在两个点电荷之间，周期为( 即前面的所说的“真空背景周期”)。运动电荷对应的电流可认为就是位移电流，这种运动使两个电荷间的电场也发生了周期性的变化，变化的周期也为t。由于位移电流的本质就是变化的电场，则 e/t 在数值上可表示电流的空间分布，电流方向垂直于以 r 为半径的球面，式中的横截面积为s =4πr2。

由于系统处在真空之中，电阻率很大(相对于导体来说) ，但电子的运动是自由的，两个点电荷间的电阻为：

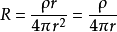
一个电荷相对一另一个电荷的电势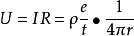 ，相对应的电势能为

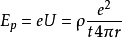
比较势能表达式可知 ε0= t / p，表明真空介电常数 ε0与真空背景周期成正比。如果假定电阻率 ρ =1，真空背景周期与真空介电常数在数值上完全相等。可得：

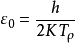
上式说明真空背景温度与真空介电常数成反比，这个结果也显示现实真空环境与宇宙背景有直接关系.虽然用 e/t 来表示位移电流的空间分布并不严格，但是足以说明真空介电常数的测量值与宇宙背景温度有很大程度的关联。2