简介绝热过程
绝热过程就是在状态变化过程中,系统与环境之间没有热交换的过程。实际上真正的绝热过程是不存在的,但是可以把在隔热性能较好的密闭容器内发生的状态变化过程近似看作绝热过程。有时虽然容器的绝热性能不是很好,但是其中的状态变化过程或化学反应在很短的时间内就能完成,在此期间由于时间短,系统与环境交换的热量很少,必要时也可以把这种过程近似看作绝热过程。1
基本公式对于封闭系统绝热过程,因Q=0,则由热力学第一定律数学表达式可得:
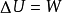
无论绝热过程是否可逆,上式均可成立。对于纯理想气体封闭系统的绝热过程,则由上式得:
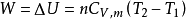
上式表明,在绝热过程中,系统对外做功(如绝热膨胀),需要消耗系统的热力学能,系统温度必然降低;系统得到功(如绝热压缩),将使系统的热力学能增加,系统温度必然升高。2
可逆绝热过程方程使用条件(1)理想气体封闭系统;
(2) ;
;
(3)可逆;
(4)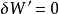 。2
。2
具体方程式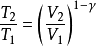
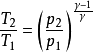
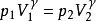 其中:
其中:
(1)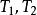 表示系统始、终态的温度,K;
表示系统始、终态的温度,K;
(2)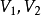 表示系统始、终态的体积,
表示系统始、终态的体积,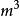 ;
;
(3)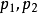 表示系统始、终态的压力,Pa;
表示系统始、终态的压力,Pa;
(4)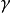 表示绝热指数或热容商,
表示绝热指数或热容商,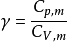 。2
。2
功能在理想气体的可逆绝热过程中,若已知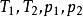 或
或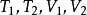 或
或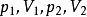 中任意三个量,利用上述方程式,就可以求第四个量,进而可以求得
中任意三个量,利用上述方程式,就可以求第四个量,进而可以求得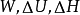 。2
。2
典例例12.0mol理想气体从始态202.65kPa、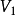 恒温可逆膨胀到
恒温可逆膨胀到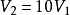 ,对外做功41.85kJ,求系统的温度和始态体积。2
,对外做功41.85kJ,求系统的温度和始态体积。2
解:根据
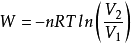
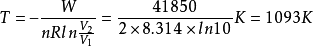
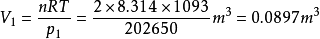
最终得系统的温度和始态体积分别为1093K和0.0897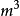 。
。
例2某理想气体2.00mol从始态298K、200kPa,恒温可逆膨胀到0.100 ,求过程的功。2
,求过程的功。2
解:对理想气体恒温可逆膨胀过程
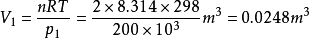
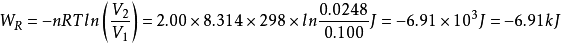
故此理想气体在该恒温可逆膨胀过程中,对环境做功6.91kJ。
例31.00mol单原子理想气体在298K、1.00×10^3kPa下可逆绝热膨胀到终态,压力为100kPa,求算终态体积、终态温度及所做的功、△U和△H。2
解:已知单原子理想气体的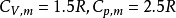 ,故
,故
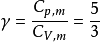
则
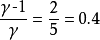
根据可逆绝热过程的方程可求得终态温度
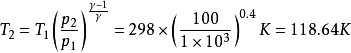
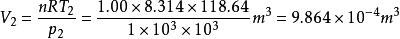
故有:

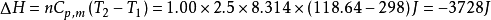




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国