[科普中国]-积分变结构控制

所谓变结构，是指当系统的状态满足一定的条件时，系统的控制结构将发生变化。变结构控制(VSC)就是当系统状态穿越不同区域时，反馈控制的结构按照一定的规律发生变化，使得控制系统对被控对象的内在参数变化和外部环境扰动等因素具有一定的适应能力，保证系统性能达到期望的性能指标要求。

由于变结构控制具有抗扰性、自适应性、鲁棒性、实现容易等优点，因此变结构控制引起了人们的普遍重视。

变结构控制的研究始于 20 世纪 50 年代，前苏联学者 Emelyanov 等提出了变结构控制概念。随后 Utkin，Itkis 等学者总结并发展了滑模变结构控制理论，奠定了滑模变结构控制的理论基础。20 世纪 80 年代以来，随着确定切换函数的系统性方法的出现和微分几何理论的发展，变结构控制开始了新的发展阶段。近二十年来，随着计算机技术和大功率电子开关器件的发展，变结构控制的实现变得越来越容易，因此该方法受到了国内外控制界的广泛重视，现已成为自动控制领域的重要设计方法，并在工程应用中得到了推广应用。

变结构控制是指系统状态达到切换函数值，系统从一个结构自动地切换到另一个确定的结构(结构是一组数学方程描述的模型)。从本质上讲它具有开关切换特性，是一种控制系统的设计方法，适用于线性及非线性系统，包括控制系统的调节，跟踪，自适应及不确定等系统。它具有一些优良特性，尤其是对加给系统的摄动和干扰有良好的自适应性。

图 1对变结构控制作了大致的分类，变结构控制可分为两大类：

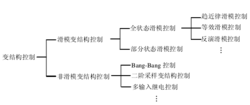
一类是不具有滑动模态的变结构控制，如Bang-Bang 控制、输出反馈变结构控制、多输入继电控制等。这一类控制只能称为变结构控制，虽然控制器可根据反馈量改变系统的结构使系统稳定于平衡位置，但系统不存在一个可滑动的面。

另一类是具有滑动模态(简称为滑模或滑模面)的变结构控制。这一类控制可称为滑模变结构控制或滑模控制，它的控制分为两个步骤：首先是系统从初始状态趋近于并到达滑模面，接着系统在滑模面上滑动并到达平衡位置。

变结构控制器都有一个切换面，如 x1，x2或者 x1+5x2，而具有滑动模态的切换面才称为滑模面。

积分控制是指控制器输出的控制信号岸(￡)与其偏差输入信号P(￡)随时间的积累值成比例。1

积分控制的传递函数为

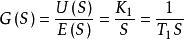
积分控制的阶跃响应为

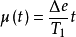
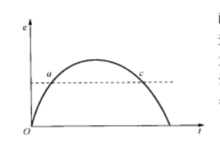
其阶跃响应曲线如图所示，由图可见，积分时间Ti表示输出量肛从开始变化到与输入量相等时所需要的时间。

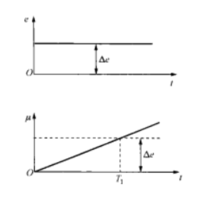
积分控制的特点是无差控制，与比例控制的有差控制形成鲜明对比。式子表明，只有当被控量偏差e为零时，积分控制器的输出才会保持不变，与此同时，控制器的输出可以停在任何数值上。这意味着被控对象在负荷扰动下的控制过程结束后，被控量没有静态偏差，而调节阀则可以停在新的负荷所要求的开度上。

采用积分控制的控制系统，其调节阀开度与当时被控量的数值本身没有直接关系，因此，积分控制也称为浮动控制。

采用积分控制时，控制系统的开环增益与积分时间Ti成反比。因此，减小积分时间将增大系统的开环增益，会降低控制系统的稳定程度，直到最后出现发散的振荡过程。这从直观上也是不难理解的，因为积分时间TI越小，积分作用越强，则调节阀的动作越快，就越容易引起和加剧振荡。但与此同时，振荡频率将越来越高，而最大动态偏差则越来越小。被控量最后都没有静态偏差，这是积分控制的特点。当积分时间TI太小时，积分作用过强，容易引起和加剧振荡，甚至不稳定，但同时，振荡频率将增高，而最大动态偏差则减小，见图(a)。当积分时间TI太大时，积分作用过弱，最大动态偏差将很大，但同时振荡频率将很小，见图(c)。可见，积分时间TI。不宜过大也不宜过小，要兼顾最大动态偏差和振荡频率，积分时间T-要取合适的值，见图(b)。

积分作用虽然能实现无差调节，但它往往导致系统发生振荡。分析图中的a、c两点，由于偏差的大小方向相同，积分作用将使输出的控制作用加强，且大小相同。但a、c两点代表的过程状态并不完全相同。在a点时，偏差在上升，此时加强控制作用是正确的。在c点时，偏差虽然也为正，但偏差在下降，此时继续加强控制作用将会导致过调，控制过程产生振荡。因此，一般不单独采用积分控制器，而将它与比例作用结合构成比例积分(PI)控制器。

考虑如下不确定线性被控对象的状态方程

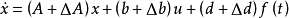
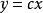
其中，x∈R”，u∈R1和f∈R1分别为系统的状态向量，控制输入和扰动信号。矩阵A和b为被控对象标称系统的参数矩阵，且{A．b}完全可控；而△A和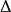b为其相应的参数摄动矩阵。2

假设：被控系统的不确定性因素△A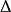，b，d和Ad满足如下的匹配条件，即根据上面的假设，系统的状态方程式则可以写为

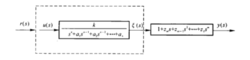
为了设计一个积分变结构滑动面。首先选择一个满足设计要求的传递函数Ⅲ，假设控制对象的标称系统传递函数有棚个零点，表示为

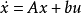
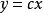
其中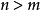，。根据图取系统的辅助输出，为了确定辅助输出，给出下面引理。

分散变结构控制的特点就在于控制量的非线性切换。这样的切换控制需要两方面的 设 计 ：

一 是 选 择 切 换 面 ， 如 全 状 态 滑 模 变 结 构 的 切 换 面 一 般 是，部分状态滑模变结构的切换面只是一部分状态反馈的线性组合，而非滑模变结构的切换面一般是某一个状态反馈；

二是切换控制律，它一般表示，其中 K(x)为切换项增益，f (s(x))为切换控制器，常用的切换控制器有理想继电器、滞环继电器等，是最常用的切换控制律。

滑模面的设计是滑模变结构控制的核心问题。滑模面设计的好坏决定系统的性能，它同时还关系到系统的稳定性和抖振的大小。滑模面的设计方法较多，具有代表性的方法有基于降阶的滑模面设计、基于线性矩阵不等式(LMI)的滑模面设计、时变滑模面设计等。

非滑模变结构切换面的设计具有更强的灵活性，同时也需要利用多种手段来分析它们。学者 Boiko、Huang、Oliveira、Plestan 提出了多种切换面设计方法，也考虑了切换面与系统的稳定关系。

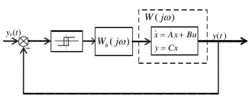
图 2、图3列出了 Boiko 提出的两种控制方法。Boiko 采用描述函数(DF)法和 LPRS 法分析它们的稳定性。图 2控制器将系统输出作为切换面，Boiko 利用 DF 法分析滞环继电器和 W(jω)的幅相频率特性。若无法得到期望的性能，则设计补偿环节，调节 W(jω)的幅相频率特性的分布。

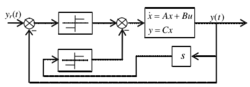
图 3将系统输出 y(t)及其导数y'(t)作为控制器的两个切换面，通过改变两继电器增益，可使其描述函数在第二象限旋转，从而改善系统控制精度。

切换控制器关系到系统鲁棒性和抖振特性。常用的切换控制器类型有理想继电器、饱和函数、滞环继电器、2-SMC等。

(1) 理想继电器是最常用的切换控制器，系统状态一旦穿越切换面，理想继电器就输出反向控制量，因此具有很好的鲁棒性，但它容易受到噪声的影响，且易引入较快的抖振频率。

(2) 饱和函数抑制抖振的效果明显，但它可能使滑模控制失去鲁棒性。

(3)滞环继电器使切换控制器变得相对迟钝，增大了切换面宽度，降低了控制精度，但通过改变迟滞量可调节抖振幅度和频率。

(4)2-SMC 具有多个控制参数，通过改变这些参数可更加灵活地调节控制器的鲁棒性和抖振特性，抖振频率既能降低也能提高。