[科普中国]-广义冯·米赛斯屈服准则

数学表达式

在一定的变形条件下，当受力物体内一点的应力偏张力的第二不变量达到某一定值时，该点就开始进入塑性状态。即

用主应力表示为:

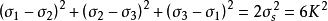
式中

σs——材料的屈服点

K ——材料的剪切屈服强度

与等效应力比较，可得

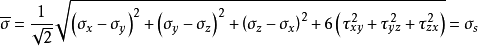
所以，广义冯·米赛斯屈服准则也可以表述为：在一定的变形条件下，当受力物体内一点的等效应力达到某一定值时，该点就开始进入塑性状态。1

米塞斯应力在弹塑性有限元计算中，屈服准则的数学描述是整个计算的核心。因此有人将等效应力叫 做von Mises应力。因此大家在弹塑性力学的书里查不到von Mises应力的定义。这是有限元软件里的一种叫法。它等同于等效应力，又称应力强度。

stress intensity（应力强度），是由第三强度理论得到的当量应力，其值为第一主应力减去第三主应力。Von Mises是一种屈服准则,屈服准则的值我们通常叫等效应力。Ansys后处理中"Von Mises Stress"我们习惯称Mises等效应力，它遵循材料力学第四强度理论(形状改变比能理论)。

第三强度理论认为最大剪应力是引起流动破坏的主要原因，如低碳钢拉伸时在与轴线成45度的截面上发生最大剪应力，材料沿着这个平面发生滑移，出现滑移线。这一理论比较好的解释了塑性材料出现塑性变形的现象。形式简单，但结果偏于安全。第四强度理论认为形状改变比能是引起材料流动破坏的主要原因。结果更符合实际。

一般脆性材料，铸铁、石料、混凝土，多用第一强度理论。考察绝对值最大的主应力。

一般材料在外力作用下产生塑性变形，以流动形式破坏时，应该采用第三或第四强度理论。压力容器上用第三强度理论（安全第一），其它多用第四强度理论。

第四强度理论应力，即mises（米塞斯）等效应力作为衡量应力水平的主要指标。mises应力是正应力和剪切应力的组合，常用来描绘联合作用的复杂应力状态。

mises stress的确是一种等效应力，它用应力等值线来表示模型内部的应力分布情况，它可以清晰描述出一种结果在整个模型中的变化，从而使分析人员可以快速的确定模型中的最危险区域。 它是根据第四强度理论计算的，因为它的计算公式是第四强度理论。

首先介绍一下形状改变比能，然后看看强度条件的推导。

物体在外力作用下会发生变形，这里所说的变形，既包括有体积改变也包括有形状改变。当物体因外力作用而产生弹性变形时，外力在相应的位移上就作了功，同时在物体内部也就积蓄了能量。例如钟表的发条(弹性体)被用力拧紧(发生变形)，此外力所作的功就转变为发条所积蓄的能。在放松过程中，发条靠它所积蓄的能使齿轮系统和指针持续转动，这时发条又对外作了功。这种随着弹性体发生变形而积蓄在其内部的能量称为变形能。在单位变形体体积内所积蓄的变形能称为变形比能。

由于物体在外力作用下所发生的弹性变形既包括物体的体积改变，也包括物体的形状改变，所以可推断，弹性体内所积蓄的变形比能也应该分成两部分：一部分是形状改变比能 ，一部分是体积改变比能。1

物理意义在一定的变形条件下，当材料的单位体积形状改变的弹性位能（又称弹性形变能）达到某一常数时，材料就屈服。

冯·米赛斯应力是基于剪切应变能的一种等效应力其值为：

其中a1,a2,a3分别指第一、二、三主应力。

冯·米赛斯应力就是一种当量应力，它是根据第四强度理论得到的当量应力。 von mises stress 是综合的概念，考虑了第一第二第三主应力，可以用来对疲劳，破坏等的评价。 YIELDING criterion （材料屈服标准）有基于stress analysis也有基于strain analysis的。 von mises stress（VMS）其实是一个STRESS yielding criterion.

我们认为对于某一材料来说，它都有一个yielding stress, 这个yielding stress 对应于相应的屈服点(yielding point)。

当材料受到外力刺激，如果其内部某处应力(VMS)大于这个yielding stress, 那么我们认为材料在此处有可能发生屈服。

Von Mises应力与Von MIses屈服准则，用在各向同性材料中较常见，来自于应力张量第一不变量。如果生物力学计算中缺乏材料数据，以近似材料参数代替，这种情况下似乎用VON应力也是可以的。

vms是材料力学中的第四屈服理论，主要是对塑性材料的，考虑的主要是疲劳效应。最大应力，最大应变主要是针对脆性材料的。1

特点广义冯·米赛斯屈服准则具有如下优缺点:

优点：

（1）考虑了中主应力σ2对屈服和破坏的影响；

（2）简单实用，材料参数少，易于实验测定；

（3）屈服曲面光滑，没有棱角，利于塑性应变增量方向的确定和数值计算。

缺点：

（1）没有考虑静水压力对屈服的影响；

（2）没有考虑单纯静水压力p对岩土类材料屈服的影响及屈服与破坏的非线性特性；

（3）没有考虑岩土类材料在偏平面上拉压强度不同的S-D效应，适用于金属材料。1