[科普中国]-分辨极限

定义

如图的光学系统，物是由两个辐射强度相等的不相干点光源所组成。这个光学系统是衍射受限的，意恩是，两点的象几乎恰好都是孔径的夫琅和费衍射图样。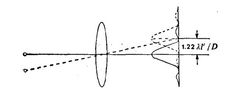

当两点问的距离很远时，两个衍射图样也同样相距很远，我们能够清楚地分辨两点。当两点互相移近时，有限扩展的衍射图样就会重迭起来。当重迭足够大时，两点就不能分辨了。

我们现在研究两个象的分辨极限问题。这就是分清两点的两个衍射图样阀的最小距离。通常应用瑞利判据，它规定当一点的衍射极大与另一点的第一衍射极小相重合时，刚好能分辨两点。

即使透镜没有象差，一个物点的成象也并不是被透镜折射的诸光线的简单相交，而是呈现一种衍射图样，因此，透镜的分辨有一个最终极限。如果一透镜或一光学系统能把两物点的相应衍射图样分得足够开，我们就说它们能分辨这两个物点。1

分辨极限的判定光学成象系统或单透镜对两个靠得很近的物的成象，如图所示。假设透镜是消象散的，即从物点S出射到透镜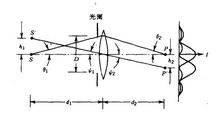上的任何一条光线都将通过象点P，且所有从S到P的光程都相等(光程长度用光波长量度)。尽管通过透镜中心的光线的几何长度比从S到P的其它光线的长度都短，但因为透镜中心较厚，故各光程的波长数是相等的。因为透镜的折射率较高，所以光波在透镜中的传播比在空气中要慢。

除了对折射光线作几何追迹外，也要考虑衍射存在，此时，透镜可视为一圆形开孔，该开孔在远场条件下产生衍射，其结果是在P和P'点所成的象不很清晰，围绕该两点各有一个远场的圆形衍射斑，因此，当两个物点靠得很近时，物点的象就叠加在一起，因此要问：物体靠得多近尚能被分辨?

瑞利判据指出，两个等亮度的物点，如果其中之一的象的衍射斑中央最大正好落在另一衍射斑的第一个最小上，即其暗环上，则说这两个物点能被光学系统的镜头所分辨。换句话说，两个衍射图样中心的距离应该等于中心亮斑的半径。

现再看上图，其中象点P和P‘的辐照度曲线表示在右边，最小可分辨角间距可写成

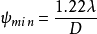
其中D是开孔的直径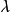， 是光源的波长。因此，按瑞利判据，如果分辨角 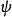小于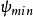 ，象就无法分辨。2

显微镜的分辨极限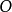两个强度相同的光点A和B，它们位于用显微镜检查的物平面上(如图）。显微镜由物镜(圆孔径)和目镜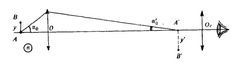 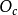组成．设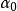 是A点对物镜半径所张的角，n是介质的折射率，乘积 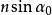是显微镜物镜的数值孔径。其实，显微镜的物镜是由几块透镜组成的，角 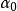是A点对第一个透镜(正面透镜)的半径所张的角。和前面一样，A和B的像是中心A'和B'(A和B的几何像)的两个衍射斑点。如果这两个斑点中心的距离 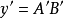由(式表示：

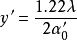
则在分辨极限内．显微镜的物镜总是满足正弦条件(阿培条件)，并可以写成

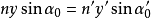
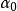其中y是物平面上两点之间的距离AB，n'是像空间的折射率。在显微镜里，角总是小的，而且n'=1。因此有

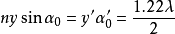
由此得出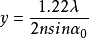 .3