[科普中国]-液化势评价

背景

我国建筑抗震设计规范(GBJ11-89)以及刚修订的抗震设计规范GB50011-2016都建议采用SPT简化方法，北美、欧洲等则大都采用基于CPT的简化评价体系。由于多次地震实测资料积累了大量SPT数据，基于SPT的液化简便评价方法目前仍然是一种较为可靠的方法。Seed提出的液化评价简化方法已成为北美、欧洲液化评价方法的范式。多年以来，国内不少学者探讨了液化判别的概率方法，但对液化势或液化危害性概率评价则少有涉足。由于以下几个方面的原因，建立场地液化势评价概率模型显得尤为必要。第一，土是一种强非均质性的材料，其材料属性大都应作为随机变量或空间随机变量处理。第二，所谓的液化指数仅表明液化发生后液化效应大小，不能反映液化的可能性。第三，随着抗震设计理论的发展，基础设计、上部结构设计都以概率为设计准则，显然在地基方面仍然采用确定性方法不能使结构设计统一在一个原则上，即都以概率为设计准则。

基于世界范围内多次地震特别是近几年发生的几次大地震实测资料，利用人工神经网络(ANN)模型来搜寻SPT与抗液化能力之间的非线性关系(液化极限状态方程)。利用概率理论建立液化评价概率模型，在此基础之上，提出了与我国规范相适应的液化严重指数概念和与此相适应的液化势(液化危害性)分级建议。1

理论基础最优化理论是应用数学的一个重要分支，广泛应用于各行业的系统管理、设计和决策。最优化(optimization)一般是指在某种状况下作出最好的决策或从几个候选方案中选出最佳的，其中适于非光滑及导数表达式复杂或写不出等情形的优化搜索法，是通过试取点函数值的比较来使包含极值的搜索区间缩小，并当其缩至一定程度时，区间上各点都接近所需要求的极值，则可看作极值的近似，其有黄金分割优选法和Fibonacci最优化法(Fibonaccioptimizationmethod，缩写FOM)。

Fibonacci最优化法是Kierer于1953年提出的，又称分数法，其是基于Fibonacci数列选择试取点的优化搜索法。

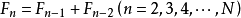
其中F0=1，F1=1。若所有可能试验总数为某个Fn-1，先选取Fn-1，Fn-2两点作为试取点并比较结果，如果第Fn-1点好，则舍去第Fn-2点以下的试验范围；若第Fn-2点好，则划去第Fn-1点以上试验范围，故新试验范围内还剩下Fn-1-1个试验点。重新编号后，第F′n-2或第F′n-1是上步留下的好点，另一个是新试验点，比较结果并作同上选择。重复以上步骤直至试验范围内没有该选的点。

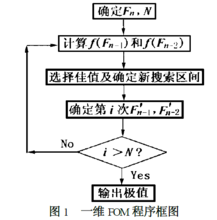
若所有可能试验总数大于某一个Fn-1而小于Fn+1-1，则先虚设几个试验点，凑成Fn+1-1个试验点即可化为前种情况，且设虚设点的试验结果比其它试取点效果差，可见增加虚设点并未增加试验次数。图1给出了求解一维函数f(x)，极值在{1，2，3，⋯，M}整数集中的FOM程序框图。1

评价指标理论研究和实地调查表明地震砂土液化受诸多因素控制，如砂土的平均粒径和相对密度、地下水水位、地震级数及持续时间等，且每个因素的影响水平是不同的。现场易于获取的、可靠的主要因素为评价指标，即地震级数M、地面水平加速度amax、粘粒含量F、平均粒径D50、上覆垂直有效应力σ′v、实测标贯击数(SPT)N。1

评价模型前人研究表明砂土液化势指数是基于经验的液化灵敏度指数，即是各影响因素的线性或非线性函数，则砂土液化的评价可看作一个多元函数最小值的最优化问题，并用多因素的FOM法来求解，即：

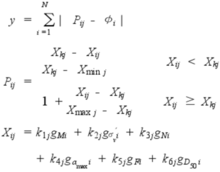
式中 y为目标函数；Pij为砂土液化预测值；φi为砂土是否液化实际值；Xkj为优化搜索值；k1，k2，k3，k4，k5，k6为{1，2，3，⋯，N}正整数集合中的点；gMi，gamaxi，gσ′vi，gD50i，gFi，gNi为评价点的M，amax，σ′v，D50，F，N经数据预处理后的数值。2

液化极限状态方程Juang与前人所用统计分析方法不同，而是基于多次地震场地液化性状实例采用非线性映射能力强的BP神经网络建立预测模型，通过搜寻算法来建立标贯击数与抗液化能力之间的非线性关系(液化极限状态方程)。然而，液化性状实例库中没有将中国几次主要地震搜集在内。此外Juang建议的搜寻算法并不一定得到理想的结果。在该液化性状实例库基础上添加了中国包括通海、海城和唐山几次大地震场地液化性状实测资料，共297个场地液化实测资料，其中液化184个，非液化场地113个。对于SPT标贯击数，由于杆长，能量比，细粒含量对其都有一定影响，所以对实测的标贯击数一般应进行修正。Seed曾说明中国标贯试验的能量比接近60%，故不进行能量修正。其它诸如杆长等修正项本文由于资料不全而不予考虑。对于细粒含量采用Idriss所建立的方法，即方程(N1)60，cs=α+β(N1)60对SPT实测值进行转换。地震的循环应力比可由Seed建议的经验公式进行计算:

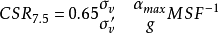
式中:MSF=(MW/7.5)-2.56；αmax=峰值加速度；σv、σ′v分别为总应力和有效应力；MW为矩震级。

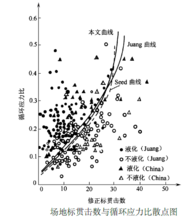右图为297 个场地液化实测数据计算出的修正标贯值与循环应力比(CRR715 ) 散点图。从图中可以看出， 液化与不液化点可用图中的实曲线来区分， 该曲线Juang 称为液化极限状态方程。

采用径向基网络算法， 来搜寻液化与非液化分界点。径向基函数(RBF) 是一种典型的局部逼近网络， 在逼近能力、分类能力等方面均优于BP 网络。

网络训练及测试结果表明径向基网络适用于非线性分类问题。平均判别成功率大于93 %。利用训练好的网络， 对每一个样本进行测试， 若液化则减小循环应力比直至输出结果为非液化； 反之， 则增加循环应力比直至输出结果为液化。将所有样本液化性质转变点的标贯击数和循环应力比进行曲线拟合。1