[科普中国]-全状态反馈控制

利用系统输出信息或状态信息反馈到系统的输入，并与系统的参考输入一起，组成一定的控制规律来控制系统的输出响应，称为反馈控制．反馈控制主要的特点是能改变系统的极点位置，从而改变系统的动态响应．例如。采用输出反馈控制较开环控制可以提高系统抗扰动能力。可以降低系统对其内部参数变化的灵敏度；又如，采用输出负反馈，可以使原开环系统不稳定变为稳定，可以使对象惯性较大系统变得系统惯性较小，从而加快系统动态响应。全状态反馈控制可以作到使闭环系统极点为希望的极点．从而可以完全确定系统的响应性能，得到希望的动态响应特性，当然。实现系统的全状态反馈必须满足系统是完全能观测的和系统是完全能控的，实际系统要想获得状态的全部信息，大多数情况是比较困难的，因此。工程上采取比较简单办法实现反馈控制。一种办法是只采用输出信息反馈控制，另一种办法是间接实现全状态反馈控制，即应用状态观测器的状态反馈控制，也可以获得优良的控制性能。1

当受控客体受干扰的影响，其实现状态与期望状态出现偏差时，控制主体将根据这种偏差发出新的指令，以纠正偏差，抵消干扰的作用。在闭环控制中，由于控制主体能根据反馈信息发现和纠正受控客体运行的偏差，所以有较强的抗干扰能力，能进行有效的控制，从而保证预定目标的实现。管理中所实行的控制大多是闭环控制，所用的控制原理主要是反馈原理。这种控制如果我们把输入值用x表示，输出值用y表示，客体的功能用s表示，控制系统也即反馈系统的作用用R表示，偏差信息用△x表示，

则有：y=S(X+△X)=S(X+Ry)=SX+SRy

式中R称反馈因子或控制参数，它反映闭环控制系统的反馈功能或控制功能。

在闭环控制系统里，即使有干扰，也能通过自己的调节保持原来的状态。实施闭环控制的抗干扰能力来自于反馈作用。因为在组织形式上增设了一个反馈机构，能把造成偏离目标的原因以及一贯干扰的因素及时地反馈给控制者，使决策控制层作出正确的决策，随时修正目标。

闭环控制的优点是充分发挥了反馈的重要作用，排除了难以预料或不确定的因素，使校正行动更准确，更有力。但它缺乏开环控制的那种预防性。如在控制过程中造成不利的后果才采取纠正措施。

状态反馈是系统的状态变量通过比例环节传送到输入端去的反馈方式。状态反馈是体现现代控制理论特色的一种控制方式。状态变量能够全面地反映系统的内部特性，因此状态反馈比传统的输出反馈能更有效地改善系统的性能。但是状态变量往往不能从系统外部直接测量得到，这就使得状态反馈的技术实现往往比输出反馈复杂。

状态反馈是控制系统设计中的一种基本控制方式。给定线性定常系统Σ(A，B，C)，称

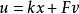
为Σ的状态反馈，其中K∈Rr×n，F∈Rr×r，且detF≠0。将上式代入原系统得闭环系统ΣC(A+BK，BF，C)。ΣC表明状态反馈改变了原系统Σ的结构，因此也就改变了原系统的动态行为。状态反馈不能改变原系统Σ的能控性，但能改变原系统Σ的能观测性。2

对系统Σ(A，B，C)，量测的通常不是全部状态x而是输出y。此时为实现状态反馈必须增加状态观测器。为了直接应用量测信息，取u=Hy+Fv，其中H∈Rr×m，F同上，通常称为输出反馈。输出反馈既不改变原系统Σ的能控性，又不改变原系统Σ的能观测性。

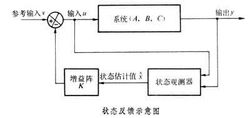
图中为状态反馈的基本形式。其中是状态变量的估计值，K是一个常系数矩阵（比例环节），通常称为反馈增益矩阵。如果原系统是定常线性系统(A，B，C),则在引入状态反馈K以后,系统就化成(A-BK，B，C)。状态反馈把系统的动态矩阵A变成A-BK,但不影响输入矩阵B和输出矩阵C。状态反馈也不影响系统的能控性，但可能改变系统的能观测性。只要原系统是能控的，则一定可以通过适当选取反馈增益矩阵K用状态反馈来任意移置闭环系统的极点(见极点配置)。对于传统的输出反馈,如果不引入附加的补偿装置，这一点不是总能作到的。

随着状态观测器理论和状态估计方法的发展（特别是由于卡尔曼-布什滤波方法的出现）,在很多情况下已不难获得状态变量的良好实时估计值，状态反馈方法已进入了实用阶段。

全状态反馈控制的主要特点是能任意配置系统极点位置，从而改善动态响应。设一个给定的n阶系统，其传递函数的n个极点的位置，能通过n个状态反馈而任意改变，那么就可以控制系统的动态响应，达到人们所希望的任意特性。但是如若实现全状态反馈。则首先要求系统的刀个状态量能够直接测量，其次．要求系统是完全能控的，上述两个条件若能满足，就可以任意地配置系统的极点。

设单输入、单输出线性定常系统的状态方程为

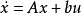
综上，根据系统要求，给定希望的闭环极点配置．就可以决定闭环系统特征多项式，从而决定全状态反馈的反馈增益矩阵足。

状态反馈闭环系统框图。如图所示。

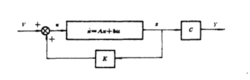
要实现全状态反馈就需要测出系统的全部状态变量，这对某些实际系统往往是困难的，或者由于传感器部件昂贵而不便采用。解决的办法是采用状态观测器间接地估计系统的状态，或者是只采用简单的输出量反馈。采用输出反馈尽管不能像全状态反馈那样可以任意配置反馈系统的极点，但只要适当地选择控制器的结构和参数，也能局部地配置系统的零极点，使闭环系统获得比较好的性能。下面将介绍状态观测器的概念。

当需要设计一个性能指标要求很高的动态系统时，就只能考虑采用全状态反馈控制。但一些实际系统的状态变量有时不易直接测量。这时就用状态观测器来估计这些不能量测的状态变量，以实现希望的全状态反馈控制。

假定被控对象是一个线性定常单变量系统，且它是完全能控与完全能观测的，系统的状态方程和输出方程为

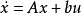
现要求依照系统的输入和输出设计一个观测器，如图所示，从图可见，观测器的输入是u，Y，而其输出是x^，要求当f→∞时观测器的输出童渐近地趋于x，

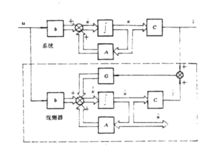
在给出性能准则意义上的最优解在于，把调节对象的全部状态并联同最优求得的增益一起反馈到这个对象的所有可能的输入端。3

这种完美的解析解法，在二次型性能准则和调节对象的线性(或线性化)微分方程情况下，不仅能提供最优调节系统普遍有效的结构及与其相关的专门与给出任务相匹配的反馈增益值，而且还能确保总系统的稳定性。由上面所列的假设(二次型性能准则，线性调节对象)还能确保只存在一个唯一的极小值，即从空间直观地把取决于调节参数的性能函数的“等高线刀想象为多维旋转椭球体。

除了这些给人以深刻印象的优点之外，该方法还存在一系列的有些还很严重的缺点：

只有线性系统的解才能以这类方法计算；如从4．3节中得到的现有的牵引系统是高度非线性的，在复杂高阶系统中进行数值计算是很困难的。

系统所有状态必须是可测量的或可观测的，这点在这里也同样办不到，或者需要较大的费用，即技术上感兴趣的准最优化系统也不能进行计算，在这种准最优化系统中不是将全部状态都反馈到全部控制量上。

一般情况下给定大量的反馈元素，目前在具有12个状态和8个输入的(4个电动机，既可以调节推力幅度，也可以调节推力方向)情况，得到12×8=96个反馈元素，这意味着设备技术的巨大耗费。

用所提到的方法不能马上考虑关于伺服量或状态量的可能约束，而且所给定的伺服电机的最大推力幅度常常仅为1000N。

状态反馈对系统能观测性的影响是指系统引入状态反馈之后系统的能观测性是否发生变化。例如，原系统是能观测的，在引入状态反馈之后，改变原来系统的能观测性，同时也有可能出现相反的情况，即引入状态反馈之后，原来不能观测的系统变成能观测的系统。

一般来说，当用状态反馈配置的系统极点与原系统的零点相同，即出现零点、极点相消时，状态反馈就改变了原来系统的能观测性。

控制理论最基本的任务是，对给定的被控系统设计能满足所期望的性能指标的闭环控制系统，即寻找反馈控制律。状态反馈和输出反馈是控制系统设计中两种主要的反馈策略，其意义分别为将观测到的状态和输出取作反馈量以构成反馈律，实现对系统的闭环控制，以达到期望的对系统的性能指标要求。在经典控制理论中，一般只考虑由系统的输出变量来构成反馈律，即输出反馈。在现代控制理论的状态空间分析方法中，多考虑采用状态变量来构成反馈律，即状态反馈。

之所以采用状态变量来构成反馈律，是因为状态空间分析中所采用的模型为状态空间模型，其状态变量可完全描述系统内部动态特性。由于由状态变量所得到的关于系统动静态的信息比输出变量提供的信息更丰富、更全面，因此，若用状态来构成反馈控制律，与用输出反馈构成的反馈控制律相比，则设计反馈律有更大的可选择的范围，而闭环系统能达到更佳的性能。另一方面，从状态空间模型输出方程可以看出，输出反馈可视为状态反馈的一个特例。因此，采用状态反馈应能达到更高的性能指标。

开环控制没有反馈环节，系统的稳定性不高,响应时间相对来说很长,精确度不高，使用于对系统稳定性精确度要求不高的简单的系统，开环控制是指控制装置与被控对象之间只有按顺序工作，没有反向联系的控制过程,按这种方式组成的系统称为开环控制系统,其特点是系统的输出量不会对系统的控制作用发生影响，没有自动修正或补偿的能力。

闭环控制有反馈环节，通过反馈系统使系统的精确度提高,响应时间缩短,适合于对系统的响应时间,稳定性要求高的系统。

半闭环控制系统是在开环控制系统的伺服机构中装有角位移检测装置，通过检测伺服机构的滚珠丝杠转角间接检测移动部件的位移，然后反馈到数控装置的比较器中，与输入原指令位移值进行比较，用比较后的差值进行控制，使移动部件补充位移，直到差值消除为止的控制系统。这种伺服机构所能达到的精度、速度和动态特性优于开环伺服机构，为大多数中小型数控机床所采用。