[科普中国]-土坡稳定分析

简介

在土木工程建筑中，如果土坡失去稳定造成塌方，不仅影响工程进度，有时还会危及人的生命安全，造成工程失事和巨大的经济损失。因此，土坡稳定问题在工程设计和施工中应引起足够的重视。

天然的斜坡、填筑的堤坝以及基坑放坡开挖等问题，都要演算斜坡的稳定性，亦既比较可能滑动面上的剪应力与抗剪强度。这种工作称为稳定性分析。土坡稳定性分析是土力学中重要的稳定分析问题。土坡失稳的类型比较复杂，大多是土体的塑性破坏。而土体塑性破坏的分析方法有极限平衡法、极限分析法和有限元法等。在边坡稳定性分析中，极限分析法和有限元法都还不够成熟。因此，目前工程实践中基本上都是采用极限平衡法。极限平衡方法分析的一般步骤是：假定斜坡破坏是沿着土体内某一确定的滑裂面滑动，根据滑裂土体的静力平衡条件和莫尔—库伦强度理论，可以计算出沿该滑裂面滑动的可能性，即土坡稳定安全系数的大小或破坏概率的高低，然后，再系统地选取许多个可能的滑动面，用同样的方法计算其稳定安全系数或破坏概率。稳定安全系数最低或者破坏概率最高的滑动面就是可能性最大的滑动面。1

土坡失稳原因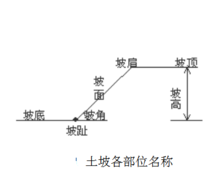土坡就是由土体构成、具有倾斜坡面的土体，它的简单外形如图所示。一般而言，土坡有两种类型。由自然地质作用所形成的土坡称为天然土坡，如山坡、江河岸坡等；由人工开挖或回填而形成的土坡称为人工土(边)坡，如基坑、土坝、路堤等的边坡。土坡在各种内力和外力的共同作用下，有可能产生剪切破坏和土体的移动。如果靠坡面处剪切破坏的面积很大，则将产生一部分土体相对于另一部分土体滑动的现象，称为滑坡。土体的滑动一般系指土坡在一定范围内整体地沿某一滑动面向下和向外移动而丧失其稳定性。除设计或施工不当可能导致土坡的失稳外，外界的不利因素影响也触发和加剧了土坡的失稳，一般有以下几种原因：

1．土坡所受的作用力发生变化：例如，由于在土坡顶部堆放材料或建造建筑物而使坡顶受荷。或由于打桩振动，车辆行驶、爆破、地震等引起的振动而改变了土坡原来的平衡状态；

2．土体抗剪强度的降低：例如，土体中含水量或超静水压力的增加；

3．静水压力的作用：例如，雨水或地面水流入土坡中的竖向裂缝，对土坡产生侧向压力，从而促进土坡产生滑动。因此，粘性土坡发生裂缝常常是土坡稳定性的不利因素，也是滑坡的预兆之一。1

无粘性土坡稳定性分析无粘性土坡即是由粗颗粒土所堆筑的土坡。相对而言，无粘性土坡的稳定性分析比较简单，可以分为下面二种情况进行讨论。

一、均质的干坡和水下坡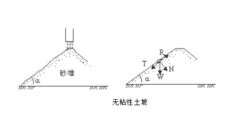均质的干坡系指由一种土组成，完全在水位以上的无粘性土坡。水下土坡亦是由一种土组成，但完全在水位以下，没有渗透水流作用的无粘性土坡。在上述二种情况下，只要土坡坡面上的土颗粒在重力作用下能够保持稳定，那么，整个土坡就是稳定的。

在无粘性土坡表面取一小块土体来进行分析(右图)，设该小块土体的重量为W，其法向分力N=Wcos，切向分力T=Wsin。法向分力产生摩擦阻力，阻止土体下滑，称为抗滑力，其值为R=N·tg=Wcos·tg。切向分力T是促使小土体下滑的滑动力。则土体的稳定安全系数Fs为：

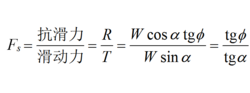
式中：

φ——土的内摩擦角(°)；

α——土坡坡角(°)。

由上式可见，当α=φ时，Fs=1，即其抗滑力等于滑动力，土坡处于极限平衡状态，此时的α就称为天然休止角。当α0的土坡，最危险滑动面的圆心位置如图(b)所示。首先按图(b)中所示的方法确定DE线。自E点向DE延线上取圆心O1、O2…，通过坡趾A分别作圆弧，AC1、AC2、…，并求出相应的边坡稳定安全系数Fs1、Fs2…。

|| || 各种坡角的β1、β2值

然后，再用适当的比例尺标在相应的圆心点上，并且连接成安全系数Fs随圆心位置的变化曲线。曲线的最低点即为圆心在DE线上时安全系数的最小值。但是真正的最危险滑弧圆心并不一定在DE线上。通过这个最低点，引DE的垂直线FG。在FG线上，在DE延线的最小值前后再定几个圆心O1'，O2'…，用类似步骤确定FG线上对应于最小安全系数的圆心，这个圆心。才被认为是通过坡趾滑出时的最危险滑动圆弧的中心。

当地基土层性质比填土软弱，或者坝坡不是单一的土坡，或者坝体填土种类不同、强度互异时，最危险的滑动面就不一定从坡趾滑出。这时寻找最危险滑动面位置就更为繁琐。实际上，对于非均质的、边界条件较为复杂的土坡，用上述方法寻找最危险滑动面的位置将是十分困难的。随着计算机技术的发展和普及，目前可以采用最优化方法，通过随机搜索，寻找最危险的滑动面的位置。国内已有这方面的程序可供使用。1

（二）边坡容许安全系数

在土坡稳定的分析中，从土体材料的强度指标到计算方法，很多因素都无法准确确定。因此，如果计算得到的土坡稳定安全系数等于1或稍大于1，并不表示边坡的稳定性能得到可靠的保证。安全系数必须满足一个最起码的要求，称为容许安全系数。容许安全系数值是以过去的工程经验为依据并以各种规范的形式确定。因此采用不同的抗剪强度试验方法和不同的稳定分析方法所得到的安全系数差别甚大，所以在应用规范所给定的土坡稳定容许安全系数时，一定要注意它所规定的试验方法和计算方法。

|| || 碾压式土石坝坝坡容许稳定安全系数

注：正常运用条件系指：

（1）水库水位处于正常高水位(或设计洪水位)与死水位之间的各种水位下的稳定渗流期；

（2）水库水位在上述范围内的经常性正常降落；

（3）抽水蓄能电站的水库水位的经常性变化和降落。

非常运用条件Ⅰ系指：

（1）施工期；

（2）校核洪水位下有可能形成稳定渗流的情况；

（3）水库水位的非常降落，如自校核洪水位降落、降落至死水位以下、大流量快速泄空等；

（4）正常运用条件遭遇地震。

非常运用条件Ⅱ系指以上非常运用条件(1)—(3)再遭遇地震的情况。

上表为1984年水电部颁布的《碾压土石坝设计规范》(SDJ218—84)中的边坡容许安全系数表。表中除注明者外，均适用于瑞典圆弧法。对Ⅰ、Ⅱ级的中、高土石坝以及一些复杂的情况，应同时采用毕肖甫法或其它更严格的方法(如普遍条分法等)进行计算。此时安全系数的容许值，应比表中所规定的值略微提高10%左右。对于Ⅰ级土石坝在正常使用条件下，安全系数不得小于1.5。1

天然土坡的稳定问题天然土体由于形成的自然环境、沉积时间以及应力历史等因素不同，性质比人工填土要复杂得多，边坡稳定分析仍然可按上述方法进行，但在强度指标的选择上要更为慎重。

一、裂隙硬粘土的边坡稳定性

硬粘土通常为超固结土，其应力—应变关系曲线属应变软化型曲线，如图所示。这类土如果也按一般的天然土坡稳定分析办法，认为剪切过程中密度不变，故宜采用不固结不排水强度指标。用φu=0法计算，得到的稳定安全系数一般过大，造成偏于不安全的结果。下表是5个已发生滑坡的这类土的天然土坡或挖方的稳定性分析实例。表中数据表明，用φu=0法分析时，稳定安全系数均很大，但实际上都发生了不稳定破坏。其原因是土坡内滑动面上的剪应力分布不均匀，各点不能同时达到破坏。破坏过程是在某些部位土的剪应力首先达到峰值，而其它部位的土尚未破坏，于是随着应变的不断加大，已经破坏部位的强度不断减小，直至变成残余强度。其它点也会相继发生这种情况，形成所谓渐进性的破坏现象。在这种情况下，边坡破坏的时间持续很长，而滑裂面的强度降至很低。有些天然滑坡体以及断层带，在其历史年代上发生过多次的滑移，经受很大的应变，土的强度下降很多。在这种情况下验算其稳定性时需注意选取其残余强度。1

|| ||

二、软土地基上土坡的稳定性分析

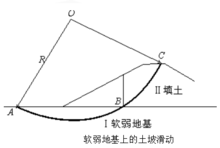在软弱地基上修筑堤坝或路基，其破坏常由地基不稳定所引起。当软土比较均匀，且厚度较大时，实地勘测和试验表明其滑动面是一个近似的圆柱面，切入地基一定深度如图中ABC所示。AB部分通过地基，BC部分通过坝体。根据瑞典圆弧法公式，Fs=MR/Ms。抗滑力矩MR由两部分组成：一是AB段上抗滑力所产生的抗滑力矩MR I；另一部分是BC段上抗滑力所产生的抗滑力矩MRⅡ。考虑到软土地基上的堤坝破坏时，在形成滑动面之前坝体一般已发生严重裂缝，或者软土地基已经破坏而坝体部分的抗剪强度尚未完全发挥。因此，如果全部计算MRⅠ和MRⅡ，求得的稳定系数偏大。为安全起见，工程中有时建议对高度在5—6m以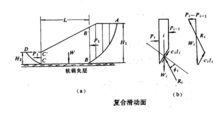下的堤防或路堤，可以不考虑坝体部分的抗滑力矩。即让MRⅡ=0，以此进行稳定分析(滑动力矩则应包括坝体部分的MsⅡ，而且是最主要的部分)。而对于中等高度的堤坝，则可考虑采用部分的MRⅡ，可根据具体工程情况并参照当地经验，采用适当的折减系数，例如用0.5。1

对于坝基内深度不大处有软弱夹层时，滑动面将不是连续的圆弧面而是由两段不同的圆弧和一段沿软弱夹层的直线所组成的复合滑动面ABCD(右图)。在这种情况下，土坡的稳定性分析可采用如下的近似方法计算。右图中滑动土体由不同圆心和半径的两段圆弧AB和CD以及软弱夹层面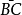组成。

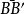用竖直线和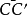将滑动土体分成ABB′、B'BCC'和C'CD三部分。第Ⅰ部分对中间第Ⅱ部分作用以推力PⅠ，第Ⅲ部分对中间第Ⅱ部分提供以抗力PⅡ。现在来分析中间部分土体B′BCC′的抗滑稳定性。其稳定安全系数可表达为：

式中：c、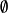——为软弱夹层土的抗剪强度指标；

W——土体B′BCC′的重量；

l——滑动面在软弱夹层上的长度；

PⅠ——土体ABB′作用于土体B′BCC′的滑动力，假定为水平方向；

PⅡ——土体CC′D对土体B′BCC′所提供的抗力，假定为水平方向。

PⅠ和PⅡ是两个待定的力，可以用作图法求之。

最后值得一提的是，无论是天然土坡还是人工土坡，在许多情况下,土体内都存在着孔隙水压力。例如, 土体内水的渗流所引起的渗透压力或者因填土而引起的超静孔隙水压力。孔隙水压力的大小在有些情况下比较容易确定，而在有些情况下则较难确定或无法确定。例如稳定渗流引起的渗透压力一般可以根据流网比较准确地确定，而在施工期、水位骤降期以及地震时产生的孔隙水压力就比较难以确定。另外，土坡在滑动过程中的孔隙水压力变化目前几乎还没有办法确定。所以，在前面所讨论的边坡稳定计算方法中，作用于滑动土体上的力是用总应力表示，还是用有效应力表示，是一个十分重要的问题。显而易见，用有效应力表示要优于用总应力表示。但是，鉴于孔隙水压力不容易确定，故而有效应力法在工程中的应用尚存在实际困难。因此，这方面的工作还有待于进一步研究。2