全驱动系统指的是系统输入数量等于被控自由度数量的一类机械系统,需要注意的是被控制自由度 数量而非系统状态数量。与之对应的两类系统为欠驱动系统与过驱动系统。对于一个给定的机械系统,其驱动情况是有具体的执行结构的配置情况决定的。1
定义牛顿形式下的描述牛顿运动定理揭示了机械系统的动力学为二阶系统。通常,这些动力学可以用如下的二阶微分方程进行描述:
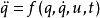 其中,
其中,
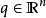 是位置状态向量,
是位置状态向量,
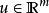 是输入状态向量,
是输入状态向量,
t是时间。
进一步地,在很多机械系统中,状态方程都可以表示成如下输入仿射的动力学
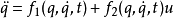
对于具有该种仿射动力学的机械系统,如满足如下的维数条件
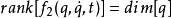
则该系统称之为全驱动系统。
端口哈密顿的描述机械系统通常均具有无源的特点,绝大多数均可以端口哈密顿(port-Hamiltonian)进行描述。基本形式如下:2
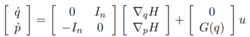
其中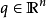 是广义位置,
是广义位置,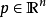 是广义动量,u是控制输入
是广义动量,u是控制输入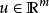 ,H为该系统的Hamiltonian函数,其定义如下
,H为该系统的Hamiltonian函数,其定义如下
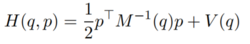
若
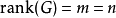
则称该机械系统为全驱动系统。
在该模型中,输入u能够影响输入矩阵G(x)的像空间Im(G(x)),在全驱动情况即可通过求解代数方程对系统进行更为灵活的成型(shaping);而欠驱动情况成型过程需要求解偏微分方程,该情况更为复杂。
物理系统举例简单机械臂考虑下图中简单的机械臂,其动力学是标准的操纵方程(manipulator equations):
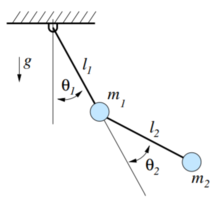 H(q)q¨ + C(q, q˙)q˙ + G(q) = B(q)u
H(q)q¨ + C(q, q˙)q˙ + G(q) = B(q)u
众所周知,惯性矩阵H(q)总是一致对称和正定的,因此可逆。这样我们可以得到
q¨ =H−1(q) [C(q, q˙)q˙ + G(q)] + H−1(q)B(q)u.
由于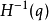 一直满秩,我们可以发现该机械系统是全驱动的,当且仅当B(q)是行满秩的。例如如下情形系统全驱动,
一直满秩,我们可以发现该机械系统是全驱动的,当且仅当B(q)是行满秩的。例如如下情形系统全驱动,
q = [θ1, θ2] T and u = [τ1, τ2] T , and B(q) = I2×2.
一些动力定位系统动力定位系统(Dynamic Positioning System)是一种闭环的控制系统,其采用推力器来提供抵抗风、浪、流等作用在船上的环境力,从而使船尽可能地保持在海平面上要求的位置上,其定位成本不会随着水深增加而增加,并且操作也比较方便。动力定位系统首先在海洋钻井船、平台支持船、潜水器支持船、管道和电缆敷设船、科学考察船、深海救生船等方面得到应用,其主要原理是利用计算机对采集来的环境参数(风、浪、流),根据位置参照系统提供的位置,自动地进行计算,控制各推力器的推力大小,使船舶保持艏向和船位的“纹丝不动”。
在一些特定情况下,动力定位系统为全驱动。动力学如下,3
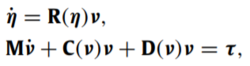
其中η是广义位置向量,ν是船体坐标系下的速度向量,τ表示总的力和力矩,M为总的广义质量矩阵,C(ν)为Coriollis矩阵,D(ν)是总的水动力阻尼矩阵,函数R(η)是旋转矩阵。如上表示形式可视为全驱动系统,其亦可转换为端口哈密顿形式,如下4
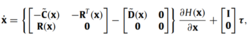




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国