[科普中国]-优化反馈控制

背景和发展

工业过程优化与运行的自动控制近年来逐渐成为控制理论与工程领域的热点研究问题。从工程实践的角度看，工业过程白动化的作用不仅仅要使关键过程变量很好地跟踪设定值的变化，实现工艺上的要求，而且要控制整个生产运行过程中反映产品质量、效率与消耗相关的指标，即运行指标在目标值范围内，实现过程运行的优化控制。1

自优化控制以工业过程的经济效益为目标函数，在满足工业过程各种约束条件的情况下，寻找合适的被控变量，用一组固定的常数作为被控变量的设定值，使实际工况处在近似最优操作点上，实际目标函数与最优目标函数的偏差处于可以接受范围内。实时优化(Real time optimization, RTO)将回路控制与过程运行的优化相结合，采用两层结构，上层在线的实时优化经济性能指标，经计算产生底层控制回路被控变量的设定值，通过底层控制器作用使被控变量跟踪设定值，从而尽可能使生产过程运行在经济优化状态。对于钢铁、有色金属等工业过程，其生产过程往往是动态的.产品牌号的变化、原料成份的波动等因素使生产过程存在各种干扰和不确定动态；另外，生产边界条件变化、各种运行设备或了系统故障、外部干扰等多种因素常常导致被控系统从一个工作点变到另一个工作点，甚至使系统参数发生大范围跳变.因此，难以采用RTO等基于稳态模型的运行优化方法。

国外高技术公司针对钢铁等工业过程采用预处理手段使原材料成份稳定、生产工况平稳，研发将运行指标转化为控制回路设定值的工艺模型或经验模型，进行开环设定控制.然而我国资源条件和生产条件与国外差别较大，原材料成份波动大，因此国外研发的控制技术及系统并不适合国情.国内学者针对

我国工业生产过程的上述问题，通常结合具体的工业过程采用基于智能技术的运行反馈控制方法。针对热轧层流冷却过程将常规控制与基于神经网络、模糊推理的智能控制技术相结合，提出了一种混合监控方法，来改善最终产品的性能。提出了基于集成控制的优化设定方法，应用于s段步进梁式加热炉，改善了粱坯的加热效果。将建模与控制相集成，反馈、预测、前馈相结合，采用案例推理、规则推理、神经网络等智能方法，提出了过程优化运行的混合智能控制方法，应用于赤铁竖炉，将运行指标控制在目标值范围内。针对铝烧结生产线的原料浆制备过程采用机理知识与智能技术，提出了基于集成模型和层次推理的设定控制方法。

然而上述自优化、RTO和智能运行反馈控制方法均假设底层过程控制可以跟踪运行控制给出的设定值，没有考虑底层跟踪设定值的动态误差对双闭环运行优化与控制的影响。结合工业过程中广泛采用的模型预测控制提出一种更常规的动态运行反馈最优控制策略，并给出了保证系统渐近稳定的充分条件。该方法针对实际流程工业过程的运行特点，提出了运行优化反馈控制的两层结构框架，并采用双闭环回路控制方法;建立关于运行指标和底层回路设定值的无限时域二次型预测控制性能指标；设计了鲁棒模型预测控制器以保证运行指标控制最优跟踪浮选过程，可以动态地给出精矿品位与尾矿品位优化设定值，当运行工况受到扰动出现波动时，通过调节作用保证浮选过程运行在目标工况下。

反馈控制简介反馈控制是控制策略的一种特殊方式。反馈控制是控制理论和控制工程中最重要的一种控制策略。它是用对象的状态或者输出来改造控制输入，使得系统有期望的性能(如图)。图中的Q是非线性算子时，称为非线性反馈控制.常用的反馈控制有动态反馈、状态反馈和输出反馈三种。

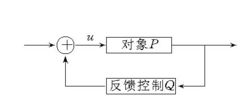
亦称“闭环控制”。一种高精度自控方法。电压、电流、速度都可闭环。由于能检测指令速度和实际速度之差而及时反馈，因此能达到控制可控硅触发角而平滑地控制速度，且平层精度高。

指作为被控的输出以一定方式返回到作为控制的输入端，并对输入端施加控制影响的一种控制关系。在控制论中，闭环通常指输出端通过“旁链”方式回馈到输入，所谓闭环控制。输出端回馈到输入端并参与对输出端再控制，这才是闭环控制的目的，这种目的是通过反馈来实现的。

区别开环控制系统：不将控制的结果反馈回来影响当前控制的系统

举例：打开灯的开关——按下开关后的一瞬间，控制活动已经结束，灯是否亮起已对按开关的这个活动没有影响；投篮——篮球出手后就无法再继续对其控制，无论球进与否，球出手的一瞬间控制活动即结束。

闭环控制系统：可以将控制的结果反馈回来与希望值比较，并根据它们的误差调整控制作用的系统

举例：调节水龙头——首先在头脑中对水流有一个期望的流量，水龙头打开后由眼睛观察现有的流量大小与期望值进行比较，并不断的用手进行调节形成一个反馈闭环控制；骑自行车——同理，不断的修正行进的方向与速度形成闭环控制。

开环闭环的区别：1、有无反馈；2、是否对当前控制起作用。开环控制一般是在瞬间就完成的控制活动，闭环控制一定会持续一定的时间，可以借此判断。

投篮第一次投篮投近了第二次投的时候用力一些，这也是一种反馈但不会对第一次产生影响了，所以是开环控制。

优化控制定义优化控制是指在给定的约束条件下，寻求一个控制系统，使给定的被控系统性能指标取得最大或最小值的控制。

随着科学技术的发展，目前智能控制已开始广泛应用。这种控制将人类的智能，例如把适应、学习、探索等能力引入控制系统，使其具有识别、决策等功能，从而使自动控制和优化控制达到了更高级的阶段。

条件一般说，进行优化控制必须要具备三个条件：

1、要给出系统的性能指标。

2、要给出约束条件。

3、要寻找优化控制的机制和方法。

由于在实际中情况是复杂多变的，进行优化控制不可能达到十全十美，因此优化控制只能是相对的或满意的控制，而难以做到最优控制。

最优控制理论最优控制理论（optimal control theory），是现代控制理论的一个主要分支，着重于研究使控制系统的性能指标实现最优化的基本条件和综合方法。 最优控制理论是研究和解决从一切可能的控制方案中寻找最优解的一门学科。它是现代控制理论的重要组成部分。

最优控制理论所研究的问题可以概括为：对一个受控的动力学系统或运动过程，从一类允许的控制方案中找出一个最优的控制方案，使系统的运动在由某个初始状态转移到指定的目标状态的同时，其性能指标值为最优。这类问题广泛存在于技术领域或社会问题中。

例如，确定一个最优控制方式使空间飞行器由一个轨道转换到另一轨道过程中燃料消耗最少，选择一个温度的调节规律和相应的原料配比使化工反应过程的产量最多，制定一项最合理的人口政策使人口发展过程中老化指数、抚养指数和劳动力指数等为最优等，都是一些典型的最优控制问题。最优控制理论是50年代中期在空间技术的推动下开始形成和发展起来的。苏联学者Л.С.庞特里亚金1958年提出的极大值原理和美国学者R.贝尔曼1956年提出的动态规划，对最优控制理论的形成和发展起了重要的作用。线性系统在二次型性能指标下的最优控制问题则是R.E.卡尔曼在60年代初提出和解决的。

系统集成集成优化控制算法及其实现网络化系统的集成优化控制方法就是将复杂系统的集成优化控制方法和网络自动化技术相结合，用来解决网络化复杂系统的优化控制问题，使其在难以建模、系统具有网络化和区域化等情况下，获得满意的优化控制结果。网络化系统集成优化控制方法的特点是引入了网络回路，在优化算法中引人了一些不确定因素，其优化控制更加依赖于网络系统和网络技术。网络化系统集成优化控制的关键技术在于动态系统优化与参数估计集成优化方法的实现和网络信息传输，借助于动态系统集成优化控制技术和网络自动化技术可实现网络化系统的集成优化控制，可以基于局域网或Intemet实现。基于局域网的网络化系统集成优化控制的示意图如下图所示。

集成优化控制的特征对一个动态优化控制方法，除了给出优化算法，还需要对其性能进行分析，只有这样才能保证优化方法的实施。网络化系统的集成优化控制方法的性能包括实时性、最优性、收敛性及其鲁棒性等。

1).实时性 在引人网络之前，针对跨区域的复杂系统，其优化控制的实施是很困难的，即使能够，其实时性也难以保证。网络化系统集成优化控制方法由于借助于计算机网络技术来实施集成优化控制，可以较好地解决跨区域复杂系统集成优化控制的实时性问题。

2).最优性 算法最优性是指在算法收敛的情况下，收敛解是否实际系统的最优解。对于网络化系统集成优化控制方法，在最优解存在且唯一等假设条件下，若算法收敛，则收敛解满足最优性必要条件，即所得优化解是实际系统的真实最优解。

3).收敛性 网络化系统集成优化控制方法需要实施，首先要求其优化控制算法是收敛的，收敛性就是研究算法收敛的条件，针对不同的算法其收敛性条件有所不同。对于网络化系统的集成优化控制方法，其优化的框架没有改变，只是引人了网络回路，利用算法映射及压缩映射原理，通过分析可以获得保证优化算法收敛的条件。

4).鲁棒性 网络化系统集成优化控制方法的鲁棒性问题是指在存在这样那样扰动的情况下，优化算法保持其收敛性，并收敛到最优解的能力。网络化系统的集成优化控制方法在不需要实际过程的精确数学模型的情况下可以获得实际系统的真实最优解，对模型的结构和参数具有较强的鲁棒性。

网络化系统的集成优化控制方法是一种基于网络环境下的集成优化控制方法，计算机网络的信息的安全问题必然影响到系统集成优化控制的实施。因此，对网络化系统集成优化控制中的信息安全问题及其对策进行分析和研究是十分必要的，只有这样才能保证网络化系统的集成优化控制的顺利实施。网络化系统集成优化控制中的信息安全问题可以借助于计算机网络的信息安全对策予以解决。

优越性网络化系统的集成优化控制方法为解决区域性复杂系统的优化控制提供了一种新思路，该方法具有以下优越性:

1)由于网络化系统的集成优化控制方法本质是采用动态大系统的DISOPE递阶优化方法，这样就使得网络化系统的集成优化控制在不需要复杂系统的精确数学模型的情况下，就可以获得实际系统的真实最优解;

2)网络化系统的集成优化控制方法为解决跨区域性的复杂系统的优化控制提供了一种可靠的实现途径和形式。同时由于网络自动化技术的发展和网络信息传输实时性的提高，使得实时地解决区域性的复杂系统的优化控制成为可能。

主要方法为了解决最优控制问题，必须建立描述受控运动过程的运动方程，给出控制变量的允许取值范围，指定运动过程的初始状态和目标状态，并且规定一个评价运动过程品质优劣的性能指标。通常，性能指标的好坏取决于所选择的控制函数和相应的运动状态。系统的运动状态受到运动方程的约束，而控制函数只能在允许的范围内选取。因此，从数学上看，确定最优控制问题可以表述为：在运动方程和允许控制范围的约束下，对以控制函数和运动状态为变量的性能指标函数（称为泛函）求取极值（极大值或极小值）。解决最优控制问题的主要方法有古典变分法、极大值原理和动态规划。

古典变分法研究对泛函求极值的一种数学方法。古典变分法只能用在控制变量的取值范围不受限制的情况。在许多实际控制问题中，控制函数的取值常常受到封闭性的边界限制，如方向舵只能在两个极限值范围内转动，电动机的力矩只能在正负的最大值范围内产生等。因此，古典变分法对于解决许多重要的实际最优控制问题，是无能为力的。

极大值原理极大值原理，是分析力学中哈密顿方法的推广。极大值原理的突出优点是可用于控制变量受限制的情况，能给出问题中最优控制所必须满足的条件。

动态规划动态规划是数学规划的一种，同样可用于控制变量受限制的情况，是一种很适合于在计算机上进行计算的比较有效的方法。

最优控制理论已被应用于最省燃料控制系统、最小能耗控制系统、线性调节器等。

优化技术最优控制的实现离不开最优化技术，最优化技术是研究和解决最优化问题的一门学科，它研究和解决如何从一切可能的方案中寻找最优的方案。也就是说，最优化技术是研究和解决如何将最优化问题表示为数学模型以及如何根据数学模型尽快求出其最优解这两大问题。一般而言，用最优化方法解决实际工程问题可分为三步进行：

①根据所提出的最优化问题，建立最优化问题的数学模型，确定变量，列出约束条件和目标函数；

②对所建立的数学模型进行具体分析和研究，选择合适的最优化方法；

③根据最优化方法的算法列出程序框图和编写程序，用计算机求出最优解，并对算法的收敛性、通用性、简便性、计算效率及误差等作出评价。

求解方法所谓最优化问题，就是寻找一个最优控制方案或最优控制规律，使系统能最优地达到预期的目标。在最优化问题的数学模型建立后，主要问题是如何通过不同的求解方法解决寻优问题。一般而言，最优化方式有离线静态优化方式和在线动态优化方式，而最优化问题的求解方法大致可分为四类：

解析法对于目标函数及约束条件具有简单而明确的数学表达式的最优化问题，通常可采用解析法来解决。其求解方法是先按照函数极值的必要条件，用数学分析方法求出其解析解，然后按照充分条件或问题的实际物理意义间接地确定最优解。

这种方法适用于性能指标及约束有明显解析表达式的情况。其一般步是先用求导方法或变分法求出最优控制的必要条件，得到一组方程或不等式，然后求解这组方程或不等式，得到最优控制的解析解即为所求的最优控制。解析法大致可分为两大类。第一类，无约束时，采用微分法或变分法。第二类，有约束时，采用极大值原理或动态规划。

（1）变分法：当控制向量不受约束时，引入哈密顿函数，应用变分法可以导出最优控制的必要条件，即正则方程、控制方程、边界条件、横截条件。

（2）极大值原理：在用变分法求解最优控制问题时，是假定控制向量u(O)不受任何限制，即容许控制集合可以看成是整个P维控制空间开集，控制变分u是任意的，同时还要求哈密顿出数H对u连续可微，但在实际工程上，控制变量往往受到一定的限制，这时可以用极大值原理来求解最优控制问题，这种方法其实是由变分法引申而来的，但由于它能应用于控制变量u(t)受边界限制的情况，并且不要求哈密顿出数H对u连续可微，因此获得了广泛的应用。

（3）动态规划：极大值原理一样，是处理控制向量限制在一定闭集内的最优控制问题的有效数学方法，它把复杂的最优控制间题变为多级决策过程的递推函数关系，其基础和核心时最优性原理即在一个多级决策问题中无论初始状态和初始决策如何，当把其中的任何一级和状态再作为初始级和初始状态时，如下的决定对与这一级开始往后的多级决策过程的一部分必定仍然是一个最优决策。因此，利用这一最优性原理必然可把一个多级决策问题化为最优的单级决策问题并且本级决策与本级以前的任何决策无关，只与本级的初始位置和初始决策有关。对于连续系统用动态规划法求最优控制问题时，可以先把连续系统离散化，用有限差分方程近似代替连续方程，然后用离散动态规划法求解。

数值解法（直接法）对于目标函数较为复杂或无明确的数学表达式或无法用解析法求解的最优化问题，通常可采用直接法来解决。直接法的基本思想，就是用直接搜索方法经过一系列的迭代以产生点的序列，使之逐步接近到最优点。直接法常常是根据经验或实验而得到的。

性能指标比较复杂或不能用变量显函数表示时，可以采用直接搜索法，经过若干次迭代搜索到最优点，数值计算法可以分为两大类：

（1）区间消去法，又称为一维搜索法，适用于求解单变量极值问题。主要有黄金分割法、多项式插值法等。

（2）爬山法，又称多维搜索法，适用于求解多变量极值问题。主要有坐标轮转法、步长加速法等。

解析与数值相结合的寻优方法（梯度型法）是一种解析与数值计算相结合的方法。主要包括两大类：一种是无约束梯度法，如陡降法、拟牛顿法等。第二类是有约束梯度法，如可行方向法、梯度投影法。

网络最优化方法这种方法以网络图作为数学模型，用图论方法进行搜索的寻优方法。2