[科普中国]-发散角

简介

光束发散角是用来衡量光束从束腰向外发散的速度。在自由空间光通信的应用中需要非常低的光束发散角。具有非常小发散角的光束，例如光束半径在很长的传输距离内接近常数，被称为准直光束。

由于波动性，光束中存在一些发散是不可避免的（假设光在各向同性介质中传输）。紧聚焦光束的发散角更大。如果一个光束发散角远大于物理上决定的发散角，那么光束就具有很差的光束质量。

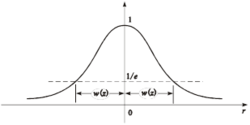
光束发散角的定量表示存在很多关于发散角的定量定义： 最常用的定义是，光束发散角为光束半径对远场轴向位置的导数，也就是与束腰的距离远大于瑞利长度。这一定义延伸出半发散角概念（单位为弧度），依赖于光束半径的定义。对于高斯光束，光束半径通常定义为处于峰值强度的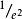 处对应的半径。而非高斯形状的光束，可以采用积分公式，在光束半径词条中有具体讨论。有时采用全角度，是半发散角的两倍。除了在高斯光束中取处于 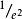峰值强度处对应的点的角度作为发散角之外，还可以采用半高全宽（FWHM）发散角。在激光二极管和发光二极管数据表格中通常采用。高斯光束中，采用这种定义的发散角是由高斯光束半径确定的半发散角的1.18倍。

举个例子，小的边发射激光二极管快轴对应的FWHM光束发散角为30°。这对应25.4° = 0.44 rad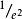 的半发射角，很显然为了在不截断它的情况下使这一光束准直需要采用相当大数值孔径的棱镜。很大发散的光束需要采用一些光学装置以避免球面象差引起的光束质量下降。

高斯光束的发散角和质量较差的光束对于衍射极限的高斯光束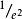， 光束半发散角为λ / (π w0)，其中 λ 是波长，w0是束腰半径。这一方程基于傍轴近似，因此只有当光束发散角不是很大时才适用。

给定光束半径，更大的光束发散角，也就是，更大的光束参数乘积，与光束质量有关，代表将光束会聚成非常小的点的可能性更小。如果用因子M来表征光束质量，那么半发散角为：

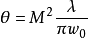
举个例子，Nd:YAG激光器产生的1064 nm的光束具有理想的光束质量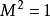（ ），光束半径为1 mm，半发散角只有 0.34 mrad = 0.019°。

空间傅里叶变换将激光光束的复电场空间进行傅里叶变换变为横向坐标的函数是非常实用的（傅里叶光学）。这样可把光束看做一系列平面波的叠加，而傅里叶变换表明平面波的振幅和相位都进行变换。在自由空间中传播时，只有相位值有变化。

空间傅里叶变换的宽度，例如均方根宽度，与光束发散角有直接关系。这表示通过计算光束轴向任一点的横向复振幅就可以得到光束发散角，这里假设光束是在各向同性介质中传播（例如空气）。

测量光束发散角为了测量光束发散角，通常测量光束散焦度，也就是采用光束分析仪测量不同位置的光束半径。

也可以从某一平面的复振幅分布来得到光束发散角。这些数据可利用夏克哈特曼波前传感器来得到。1

高斯光束由激光器产生的激光束既不是平面光波，也不是均匀的球面光波。虽然在特定位置，看似一个球面波，但它的振幅和等相位面都在变化。从理论上来讲，光在稳定的激光谐振腔中进行无限次的反射后，激光器所发出的激光将以高斯光束的形式在空间传输。而且反射（衍射）次数越多，其光束传输形状越接近高斯光束。从另一方面讲，形状越接近高斯光束的激光束，在传播、偶合及光束变换过程中，其形状越不易改变，在高斯光束时，不论怎样变换，其形状依然是高斯光束。

在激光器产生的各种模式的激光中，最基本、应用最多的是基模高斯光束。在以光束传播方向z轴为对称轴的柱面坐标系中，基模高斯光束的电矢量振动可以表示为

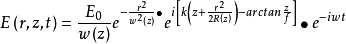
式中，E0为常数，其余各符号意义表示如下：

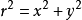
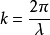
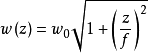
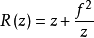
其中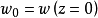， 为基模高斯光束的束腰半径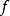， 称为高斯光束的共焦参数或瑞利长度，R(z)为与传播轴线交于z点的基模高斯光束的远场发散角为高斯光束等相位面的曲率半径，w(z) 是与传播轴线相交于z点高斯光束等相位面上的光斑半径。

根据对发散角的理解方法不同，其测量方法有很多，在此我们例举几个典型的发散角测量方法，同学们可以收集整理更多的测量方法。

透镜变换方法对高斯光束，设理想薄透镜（所谓理想薄透镜，是指在光路中引入的理想薄透镜不影响光束的强度分布，不截断光束，紧靠透镜两边的光斑大小和光强分布完全一样)的焦距为f，光腰半径为的高斯光束在透镜焦平面上的光斑半径为：

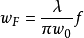
高斯光束的远场发散角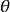为

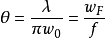
由测量实际光束在透镜后焦平面处的光斑半径wf实际，计算得到实际高斯光束远场发散角：

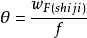
分子代表wF实际。

在会聚透镜的后焦面内测量光斑尺寸，光斑直径与聚焦透镜焦距之比即为出远场发散角。

对基模高斯光束，w为半径的环围内含有总功率的86.5%。相应的实际光束远场发散角即为其焦平面光斑中含86.5%总能量的环围的角半径。需要注意，这里测量的是透镜焦平面处的光斑，而不是透镜后的光腰尺度，光腰位置并不与焦平面重合，只有透镜焦平面处光斑才是入射光的远场。

也有采用峰值光强的1/e处的光束半径计算远场发散角的，其中含有约63.2%的总能量，这表明应用者更关心焦斑中心部分的光强。2

光强度分布测量法激光光束束腰的位置根据谐振腔腔型的不同而定，通常可以认为束腰在光束输出窗口附近。在远场时我们用光电测量装置测得光强的横向分布，确定强度为中心强度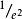处的直径d，测得测量点到束腰的距离L，则远场发散角可以认为是

在此种方法的测量中，如果是小发散角的激光光束，需要一个长的测量距离，通常可以采用平面镜多次反射的办法增加测量距离，但因为平面镜面形引起激光光束形貌改变将增加光强横向分布测量的误差。

双孔法利用两个大小一致的圆孔（光阑）相隔一定距离放在激光光路中，要求光阑与激光束腰处的直径相当，保证通过的光束能量为全部能量的86%左右。由第一个光阑发出光被第二个光阑遮挡了一部分，在第二个光阑圆孔的外围形成亮斑。如果实验条件简陋，可以直接测量这个亮斑的直径；如果有激光功率测量仪，可以分别测量两个圆孔出射的光强度，由光衍射的爱里斑换算出激光光束发散角。

由于该方法简单易行，采用此种方法测量激光光束发散角的人较多。3