下水曲线图
 船舶在下水之前必须进行下水计算并绘制下水曲线,据此可以了解该船在下水过程中是否会发生不利现象(如船尾下落或船首下落现象等),便于事先采取措施,保证安全下水。
船舶在下水之前必须进行下水计算并绘制下水曲线,据此可以了解该船在下水过程中是否会发生不利现象(如船尾下落或船首下落现象等),便于事先采取措施,保证安全下水。
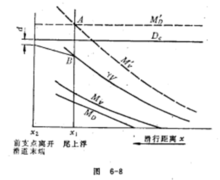
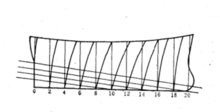
典型的下水曲线如图1所示。横坐标代表行程x,即船在底滑道上的移动距离,纵坐标为重量及力矩。下水曲线图中通常包括下列曲线:
(1)下水重量:Dc=常数(水平直线);
(2)浮力: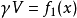 (曲线);
(曲线);
(3)下水重量对于底滑道末端的力矩: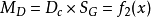 (倾斜直线);
(倾斜直线);
(4)浮力对于底滑道末端的力矩: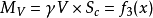 (曲线);
(曲线);
(5)下水重量对于下水架前支点的力矩: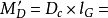 常数(水平直线);
常数(水平直线);
(6)浮力对于下水架前支点的力矩: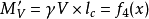 (曲线)。
(曲线)。
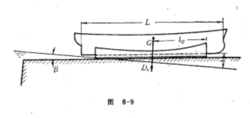 在下水曲线图上,下水重量Dc与浮力γV曲线之差即为船在不同行程时滑道的反力R。
在下水曲线图上,下水重量Dc与浮力γV曲线之差即为船在不同行程时滑道的反力R。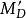 直线与
直线与 曲线的交点(图中A点)表示船尾开始上浮,与之相对应的x1表示船尾开始上浮时的行程数值。根据图中
曲线的交点(图中A点)表示船尾开始上浮,与之相对应的x1表示船尾开始上浮时的行程数值。根据图中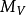 曲线与
曲线与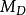 曲线可以判断船舶在下水过程中是否发生尾下落现象。若
曲线可以判断船舶在下水过程中是否发生尾下落现象。若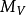 曲线位于
曲线位于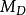 曲线之上,则表示在整个下水过程中,
曲线之上,则表示在整个下水过程中,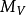 总是大于
总是大于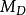 ,因而不会发生尾下落现象。图1中的γV、
,因而不会发生尾下落现象。图1中的γV、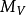 、
、 等曲线,在船尾上浮以后的那部分已没有实际意义,因为船尾上浮以后,船舶不再平行于滑道的方向运动,所以这一部分的曲线与实际情况不符。当下水进入第三阶段后,其浮力随行程的变化规律如图中的B曲线所示。设行程x2表示下水架前支点离开底滑道末端,若此时浮力小于下水重量,则将发生船首下落现象,其差数d即为下落重量。2
等曲线,在船尾上浮以后的那部分已没有实际意义,因为船尾上浮以后,船舶不再平行于滑道的方向运动,所以这一部分的曲线与实际情况不符。当下水进入第三阶段后,其浮力随行程的变化规律如图中的B曲线所示。设行程x2表示下水架前支点离开底滑道末端,若此时浮力小于下水重量,则将发生船首下落现象,其差数d即为下落重量。2
下水计算下水曲线图是根据计算结果绘制而成的,下水计算的一般步骤是:
(1)首先根据重量及重心计算的基本原理,尽可能正确地计算下水重量及重心的位置。
(2)绘制如图2所示的下水布置简图,并应注明有关尺寸。
(3)确定船舶滑行某一距离x时的首尾吃水。
设L为船舶垂线间长;α为龙骨坡度(以弧度计);β为底滑道坡度(以弧度计);h为船在未滑动时首垂线处龙骨基线在水面以上的高度。
则当船沿滑道向下滑行距离x以后,首尾吃水为:
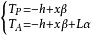
据此式可以吧船在各不同行程x(例如:x=60米、80米、100米等等)时的首尾吃水算出。
 (4)在邦戎曲线图上画出相当于上述不同行程x时的水线如图3所示。然后用近似计算法算出每一水线下的浮力γV及浮心纵向位置,据此可进一步求出浮力对于前支点及底滑道末端的力矩
(4)在邦戎曲线图上画出相当于上述不同行程x时的水线如图3所示。然后用近似计算法算出每一水线下的浮力γV及浮心纵向位置,据此可进一步求出浮力对于前支点及底滑道末端的力矩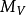 及
及 。这样,便可得出不同行程x时的γV、
。这样,便可得出不同行程x时的γV、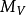 及
及 数值。同时根据下水重量Dc及重心G点的位置,可以算出
数值。同时根据下水重量Dc及重心G点的位置,可以算出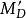 及
及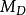 。
。
(5)既知下水重量Dc及各不同行程x时之γV、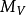 、
、 、
、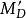 及
及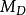 等数值,便可绘制如图1所示的下水曲线图。由
等数值,便可绘制如图1所示的下水曲线图。由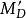 直线与
直线与 曲线的交点(图中A点)可知船尾开始上浮的位置x1.
曲线的交点(图中A点)可知船尾开始上浮的位置x1.
(6)计算船尾上浮以后的浮力。
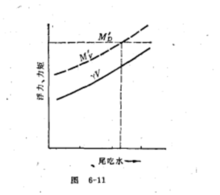 船尾上浮以后,浮力对前支点的力矩
船尾上浮以后,浮力对前支点的力矩 必等于下水重量对前支点的力矩
必等于下水重量对前支点的力矩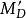 ,据此可以求出船尾上浮以后的浮力,具体的计算方法如下:先选定某一x值(应大于x1),计算船舶在前支点处的吃水。然后假定若干个尾吃水,在邦戎曲线图上画出这些水线,并量出各横剖面面积,应用近似计算方法算出每一尾吃水时的浮力、浮心位置及浮力对于前支点的力矩
,据此可以求出船尾上浮以后的浮力,具体的计算方法如下:先选定某一x值(应大于x1),计算船舶在前支点处的吃水。然后假定若干个尾吃水,在邦戎曲线图上画出这些水线,并量出各横剖面面积,应用近似计算方法算出每一尾吃水时的浮力、浮心位置及浮力对于前支点的力矩 。最后以尾吃水为横坐标,绘制浮力γV曲线,
。最后以尾吃水为横坐标,绘制浮力γV曲线, 曲线及
曲线及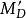 直线如图4所示。
直线如图4所示。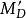 及
及 的交点即表示
的交点即表示 =
=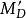 ,相当于这一交点的尾吃水即为船尾上浮以后在行程x处的船舶实际情况,其正确的浮力也可在γV曲线上查得。
,相当于这一交点的尾吃水即为船尾上浮以后在行程x处的船舶实际情况,其正确的浮力也可在γV曲线上查得。
另外再假定几个x值,同样可以算出在各x值时船舶的尾吃水和实际浮力,这样就可在下水曲线图上画出船尾上浮以后的浮力曲线,如图1中的B曲线。在行程x2(相当于前支点离开滑道末端)处,若浮力小于下水重量,则将发生船首下落现象。
(7)为了估计船只在入水后的浮态及稳性还需计算船舶下水后的首尾吃水及初稳心高度。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国